主要内容 #

1. Hanoi问题回顾
2. Hanoi问题图解
3. 编程求解

1. Hanoi问题回顾 #

汉诺塔(Tower of Hanoi)源于印度传说中，大梵天创造世界时造了三根金钢石柱子，其中一根柱子自底向上叠着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。
在之前的第119课，学习了如何使用递推方法求解汉诺塔问题：必须先求出递推公式才能求解，然而，求解汉诺塔问题更直观的方法是使用递归。

2. Hanoi问题图解 #

首先我们看一个三层汉诺塔的图解，来对汉诺塔问题的解决有做简单的回顾：

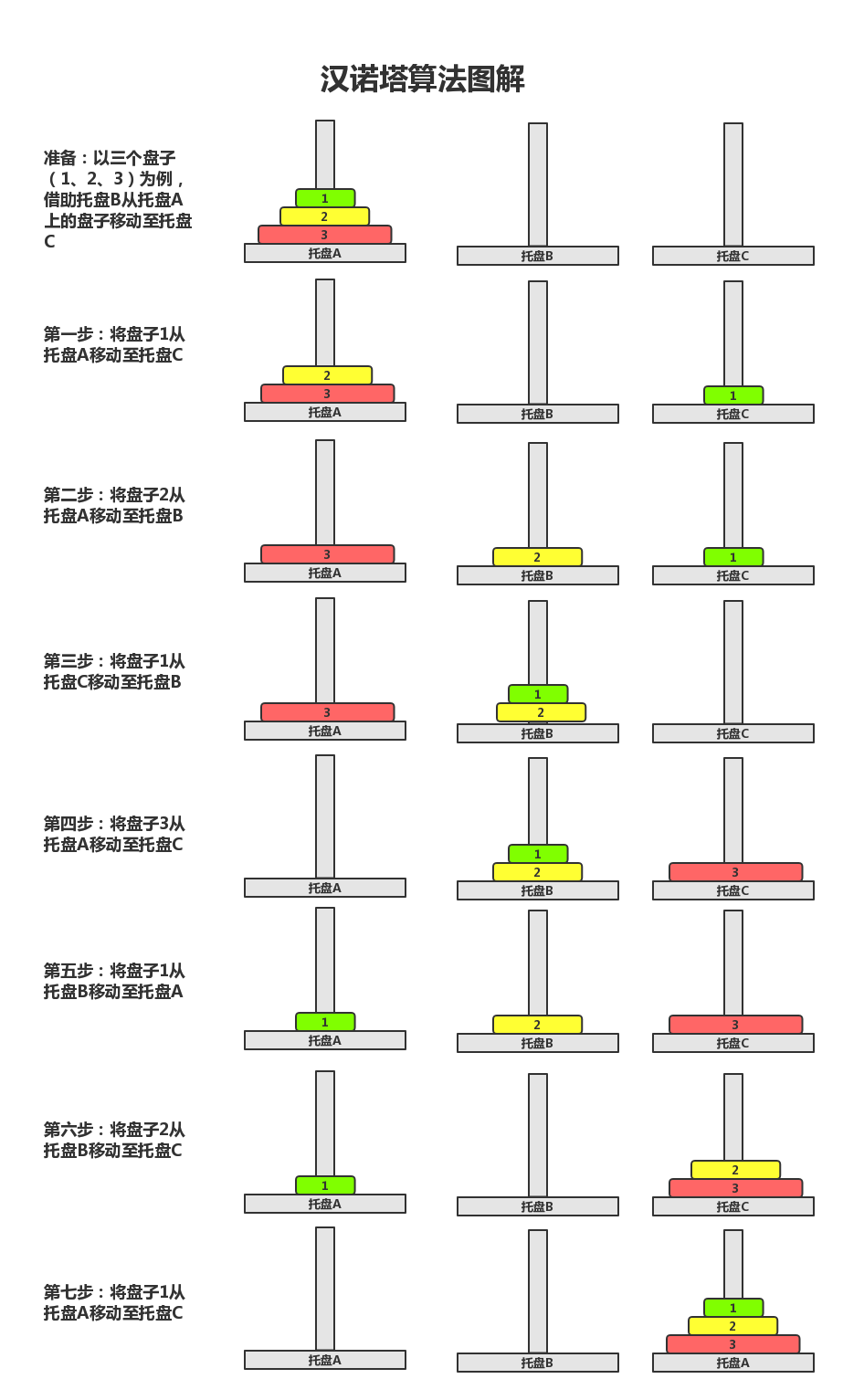
如上图所示，我们可以看出，当盘子的数量只有一个的时候，我们可以直接将盘子移动到目标盘，在进行三层汉诺塔问题的解决时。我们先将最上方的两个盘子借助目标盘移动至中转盘，再将最大的盘子移动至目标盘，之后再将中转盘上的第一个盘子移动至起始盘，这个时候我们就可以将二号盘移动至目标盘，最后将起始盘上的一号盘移动至目标盘。
由此我们可以总结出n层汉诺塔的解决方案：
将前n-1个盘子借助当前的中转盘（不一定是B托盘）移动至相邻的空托盘上，再将第n个盘子移动至目标盘，之后重复上述步骤直至将所有的盘子都移动至目标盘。在这个也用到了函数方法的递归思想。

3. 编程求解 #

参考程序

#include < iostream >
using namespace std;

void Towers(int n, char a, char b, char c){
    if(n == 1){
        cout << "移动 " << n << " 从 " << a << " 到 " << c << endl;   
    }else{
        Towers(n - 1, a, c, b);
        cout << "移动 " << n << " 从 " << a << " 到 " << c << endl; 
        Towers(n - 1, b, a, c);
    }
}
int main(){
    int n;
    cin >> n;
    Towers(n, 'A', 'B', 'C');
    cout << endl;
    return 0;
}