主要内容 #
- 递归算法回顾
- 斐波那契数列算法
- 编程求解
1. 递归算法回顾 #
程序调用自身的编程技巧称为递归(recursion)。一个方法或函数在其定义或说明中有直接或间接调用自身的一种方法,它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解,递归策略只需要少量的程序就可以描述出解题过程所需要的多次重复计算,大大地减少了程序的代码量,让程序更加的简洁。
什么样的问题才可以使用递归的方式求解呢?构成递归需要具备两个条件:
(1)子问题与原始问题属于同样的事情,二者的求解方法是相同的,且子问题比原始问题更易求解。
(2)递归不能无限制地调用本身,必须有个递归出口。递归出口对应的情形相对简单,可以化简为非递归状况处理。
2. 斐波那契数列算法 #
斐波那契数列以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:
1、1、2、3、5、8、13、21、34、……
在数学上,斐波纳契数列以如下被以递推的方法定义:
F(1)=1,F(2)=1,,F(n) = F(n-1) + F(n-2)(n>=3)。
问题分析: 斐波那契数列的对于原问题F(n)的求解可以转为对F(n-1)、F(n-2)两个子问题的求解,故符合条件(1)。由F(1)=1,F(2)=1,可以得出斐波那契数列问题是有递归出口的,递归出口对应F(1) = 1,F(2) = 1。
3. 编程求解 #
求解斐波那契数列的C语言代码如下:
#include < stdio.h >
int fibonaci(int i)
{
if(i == 0)
{
return 0;
}
if(i == 1)
{
return 1;
}
return fibonaci(i-1) + fibonaci(i-2);
}
int main()
{
int i;
for (i = 0; i < 10; i++)
{
printf("%d\t\n", fibonaci(i));
}
return 0;
}
当上面的代码被编译和执行时,它会产生下列结果:
0 1 1 2 3 5 8 13 21 34
请同学上面的C风格的代码,改写为C++风格的代码。
算法缺点:
由于使用递归时,其执行步骤是:要得到后一个数之前必须先计算出之前的两个数,即在每个递归调用时都会触发另外两个递归调用,例如:要得到F(10)之前得先得到F(9)、F(8),那么得到F(9)之前得先得到F(8)、F(7)……如此递归下去。
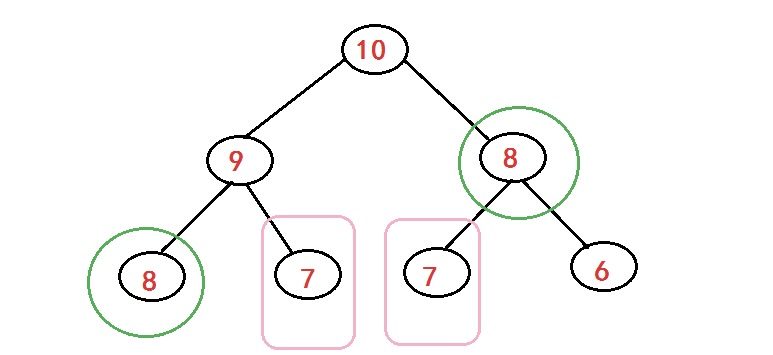
从上图可以看出,这样的计算是以 2 的次方在增长的。除此之外,也可以看到,F(8)和F(7)的值都被多次计算,如果递归的深度越深,那么F(8)和F(7)的值会被计算更多次,但是这样计算的结果都是一样的,除了其中之一外,其余的都是浪费,可想而知,这样的开销是非常恐怖的!



