主要内容 #

1. 何为递归
2. 递归求解思路
3. 案例分析

1. 何为递归 #

简单地说，就是如果在函数中存在着调用函数本身的情况，这种现象就叫递归。
以阶乘函数为例,如下, 在 factorial 函数中存在着 factorial(n – 1) 的调用，所以此函数是递归函数。

int factorial(int n) {
    if (n < =1) {
        return 1;
    }
    return n * factorial(n - 1)
}

进一步分析“递归”，先有“递”再有“归”，“递”的意思是将问题拆解成子问题来解决， 子问题再拆解成子子问题，…，直到被拆解的子问题无需再拆分成更细的子问题（即可以求解），“归”是说最小的子问题解决了，那么它的上一层子问题也就解决了，上一层的子问题解决了，上上层子问题自然也就解决了,….,直到最开始的问题解决,那以阶层 f(6) 为例来看下它的“递”和“归”。

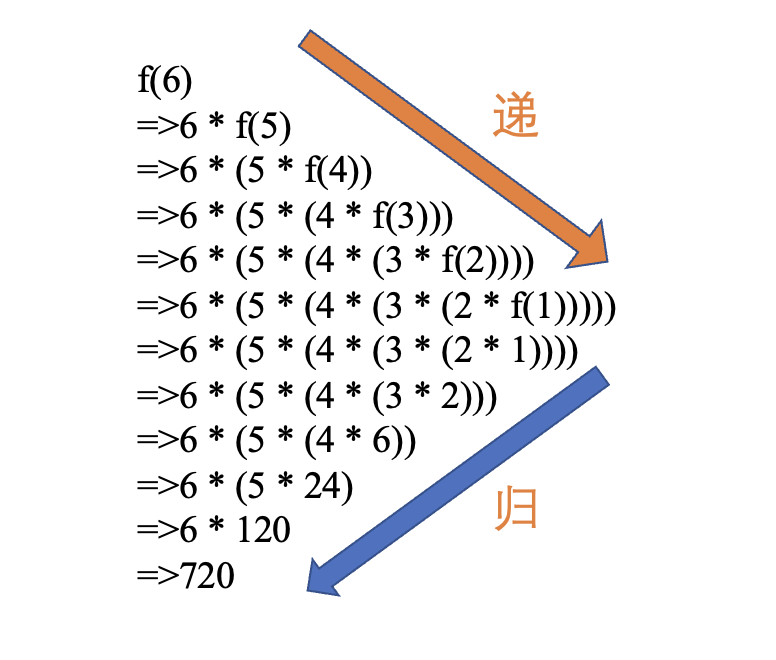
求解问题 f(6), 由于 f(6) = n * f(5), 所以 f(6) 需要拆解成 f(5) 子问题进行求解，同理 f(5) = n * f(4) ,也需要进一步拆分,… ,直到 f(1), 这是“递”，f(1) 解决了，由于 f(2) = 2 f(1) = 2 也解决了,…. f(n)到最后也解决了，这是“归”，所以递归的本质是能把问题拆分成具有相同解决思路的子问题，。。。直到最后被拆解的子问题再也不能拆分，解决了最小粒度可求解的子问题后，在“归”的过程中自然顺其自然地解决了最开始的问题。

2. 递归求解思路 #

通过以上的分析，递归有以下两个特点：

所以解递归题的关键在于我们首先需要根据以上递归的两个特点判断题目是否可以用递归来解。
经过判断可以用递归后，接下来我们就来看看用递归解题的基本套路：

2. 案例分析 #

以之前讲过的青蛙上台阶题目为例：
一只青蛙可以一次跳 1 级台阶或者一次跳 2 级台阶，例如：
跳上第 1 级台阶只有一种跳法：直接跳 1 级即可。 跳上第 2 级台阶有两种跳法：每次跳 1 级，跳两次；或者一次跳 2 级。 问要跳上第 n 级台阶有多少种跳法？
继续来按四步曲来看怎么套路
1. 定义一个函数，这个函数代表了跳上 n 级台阶的跳法：

int f(int n) {
}

2. 寻找问题与子问题之前的关系 这两者之前的关系初看确实看不出什么头绪，但仔细看题目，一只青蛙只能跳一步或两步台阶，自上而下地思考，也就是说如果要跳到 n 级台阶只能从 从 n-1 或 n-2 级跳， 所以问题就转化为跳上 n-1 和 n-2 级台阶的跳法了，如果 f(n) 代表跳到 n 级台阶的跳法，那么从以上分析可得 f(n) = f(n-1) + f(n-2),显然这就是我们要找的问题与子问题的关系,而显然当 n = 1, n = 2， 即跳一二级台阶是问题的最终解。
3. 将第二步的递推公式用代码表示出来补充到步骤 1 定义的函数中 补充后的函数如下:

/**
 * 跳 n 极台阶的跳法
 */
public int f(int n) {
    if (n == 1) return 1;
    if (n == 2) return 2;
    return f(n-1) + f(n-2)
}