主要内容 #

1. 问题描述
2. 算法思路
3. 参考程序

1. 问题描述 #

请编程完成以下任务：
1. 读取闭区间的个数及它们的描述；
2.找到一个含元素个数最少的集合,使得对于每一个区间,都至少有一个整数属于该集合，输出该集合的元素个数。
输入格式
首行包括区间的数目n,1<=n<=10000,接下来的n行,每行包括两个整数a,b,被一空格隔开,0<=a<=b<=10000,它们是某一个区间的开始值和结束值。
输出格式
第一行集合元素的个数,对于每一个区间都至少有一个整数属于该区间,且集合所包含元素数目最少。
输入样例
4
3 6
2 4
0 2
4 7
输出样例
2

2. 算法思路 #

算法模型：给n个闭区间[ai,bi], 在数轴上选尽量少的点,使每个区间内至少有一个点。
算法：首先按b1<=b2<=…<=bn排序。每次标记当前区间的右端点x，并右移当前区间指针，直到当前区间不包含x,再重复上述操作。
如下图，如果选灰色点，移动到黑色点更优。

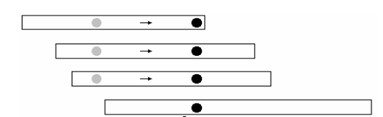
通俗的想，把区间想成一块块木板，把要找的点想成钉子，如果你的钉子很靠前的话，后面的木板就可能钉不到，每次把钉子钉在你要钉的木板最后，这样它就能顺便钉更多木板了！

3. 参考程序 #

#include<iostream>
using namespace std;
int n;
int a[10001],b[10001];
void qsort(int,int);//快排 
void slove();//解决问题 
int main()
{
    cin >> n;
    for(int i=1;i<=n;i++)
        cin >> a[i] >> b[i];
    qsort(1,n);
    slove();
    return 0;
    }
void qsort(int x,int y)
{
    int l=x,r=y,m1=(a[(x+y)/2]),m2=b[(x+y)/2];//m1为左端点的‘中间’，m2为右端点的‘中间’ 
    while(l<=r)
    {
        while(b[l]<m2||b[l]==m2&&a[l]<m1)l++;//比中间的小或者如果等于中间的并且左端点按升序排列 
        while(b[r]>m2||b[l]==m2&&a[r]>m1)r--;
        if(l<=r)//交换 
        {
            int t;
            t=b[l];b[l]=b[r];b[r]=t;
            t=a[l];a[l]=a[r];a[r]=t;
            l++;r--;
        }
    }
    if(l<y)qsort(l,r);
    if(r>x)qsort(x,r);
}
void slove()
{
    int sum=0;//x是目前的右端点 
    for(int i=1,x=-1;i<=n;i++)//x要取个负的，取0是不对的，因为区间左端点取得到0 
    {
        if(a[i]<=x)continue;//能覆盖就继续 
        sum++;x=b[i];//否则数量+1，修改目前的右端点 
    }
    cout << sum << endl;
    }