主要内容 #

1. 跳跃游戏
2. 贪心算法
3. 参考代码

1. 跳跃游戏 #

给定一个非负整数数组，你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个位置。
示例 1:
输入: [2,3,1,1,4]
输出: true
解释: 我们可以先跳 1 步，从位置 0 到达 位置 1, 然后再从位置 1 跳 3 步到达最后一个位置。
示例 2:
输入: [3,2,1,0,4]
输出: false
解释: 无论怎样，你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 ， 所以你永远不可能到达最后一个位置。

2. 贪心算法 #

刚看到本题一开始可能想：当前位置元素如果是3，我究竟是跳一步呢，还是两步呢，还是三步呢，究竟跳几步才是最优呢？
其实跳几步无所谓，关键在于可跳的覆盖范围！
不一定非要明确一次究竟跳几步，每次取最大的跳跃步数，这个就是可以跳跃的覆盖范围。
这个范围内，别管是怎么跳的，反正一定可以跳过来。
那么这个问题就转化为跳跃覆盖范围究竟可不可以覆盖到终点！
每次移动取最大跳跃步数（得到最大的覆盖范围），每移动一个单位，就更新最大覆盖范围。
贪心算法局部最优解：每次取最大跳跃步数（取最大覆盖范围），整体最优解：最后得到整体最大覆盖范围，看是否能到终点。

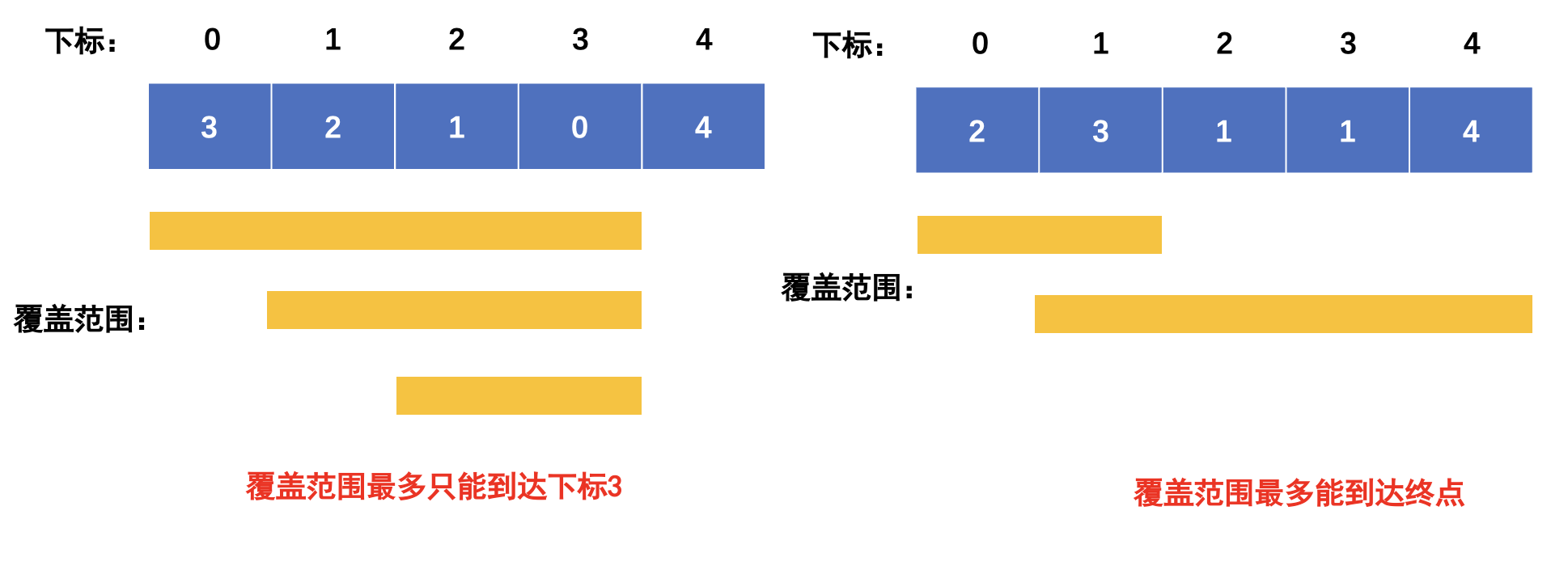
i每次移动只能在覆盖的范围内移动，每移动一个元素，覆盖范围得到该元素数值（新的覆盖范围）的补充，让i继续移动下去。
而cover每次只取 max(该元素数值补充后的范围, 覆盖范围)。
如果覆盖范围大于等于了终点下标，直接return true就可以了。

3. 参考程序 #

#include<iostream>
#include<vector>
using namespace std;

class Solution {
public:
    bool canJump(vector<int>& nums) {
        int cover = 0;
        if (nums.size() == 1) return true; // 只有一个元素，就是能达到
        for (int i = 0; i <= cover; i++) { // 注意这里是小于等于cover
            cover = max(i + nums[i], cover);
            if (cover >= nums.size() - 1) return true; // 说明可以覆盖到终点了
        }
        return false;
    }
};

int main(){
    int n;  //数组中元素的数量
    cin >> n;
    vector<int> nums; //存放输入的数据 
    while(n--){
        int num;
        cin >> num;
        nums.push_back(num);
    }
    Solution solution;
    if(solution.canJump(nums)){
        cout << "true" << endl;
    }else{
        cout << "false" << endl;
    }
    return 0;
}