主要内容 #
- 多阶段决策过程
- 最短路径问题
1. 多阶段决策过程 #
20世纪50年代初美国数学家R.E.Bellman等人在研究多阶段决策过程(multistep decision process)的优化问题时,提出了著名的最优化原理(principle of optimality),把多阶段过程转化为一系列单阶段问题,逐个求解,创立了解决这类过程优化问题的新方法——动态规划。
多阶段决策过程,是指这样的一类特殊的活动过程,问题可以按时间顺序分解成若干相互联系的阶段,在每一个阶段都要做出决策,全部过程的决策是一个决策序列。要使整个活动的总体效果达到最优的问题,称为多阶段决策问题。

2. 最短路径问题 #
多段图的最短路径问题为从源点到终点的最小代价路径。如下图所示,每条线上的数字为经过这条路径需要付出的代价,问题为选择怎样的路径才能使所付出的代价最小。
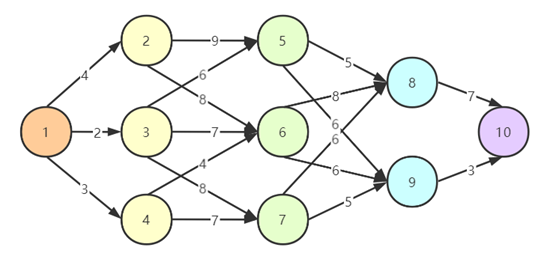
2.1 问题分析 #
根据多段图的性质,我们可以将这种特殊的图结构划分为多个子集,例如如图所示的多段图就可以分成 5 个子集,在图中以 5 种不同颜色来表示。可以明显地看到想要到达某一个子集的顶点,就必须从上一个相邻顶点集的顶点出发,不相邻的子集之间不存在可达的边。
针对这个特性可以推导出解决问题的方法,例如我想要到达顶点 10,那就必须要先到达顶点 8 或者顶点 9。换句话说,到达顶点 10 的最短距离就是在到达顶点8的最短距离 d(1,8) 加上边 (8,10) 的权重,和到达顶点 9 的最短距离 d(1,9) 加上边 (9,10) 的权重中取最小值。因为不相邻的顶点集之间不存在边,所以到达顶点 10 的方式有且仅有上述 2 种。设 C 为某条边的权重,d(m,n) 为从点 m 到点 n 的最短距离,则使用数学语言的描述如下:
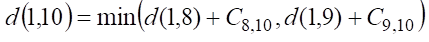
再看一个例子,假设要分析到达顶点 8 的最短距离,则只有 3 种情况。即到达顶点 5 的最短距离 d(1,5) 加上边 (5,8) 的权重,和到达顶点 6 的最短距离 d(1,6) 加上边 (6,8) 的权重,和到达顶点 7 的最短距离 d(1,7) 加上边 (7,8) 的权重三者之间取最小值。使用数学语言的描述如下:

根据上面 2 个例子的论述,我们可以把情况从特殊推广到一般情况,设 Cuv 为多段图有向边 <u,v>的权值,源点 s 到终点 v 的最短路径长为 d(s,v),终点为 t,则可以得到该问题的状态转移方程为:
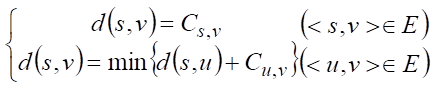
2.2 问题求解 #
例如上述例子中的多段图,可以建立图的邻接矩阵 topography.edges[MAXV][MAXV] 为:
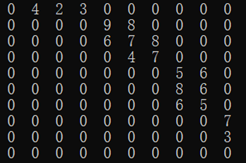
需要一个辅助结构:一维数组 cost[MAXV] 存储到每个顶点的最小开销。例如我们已经求出了到达顶点 1~9 的最小开销如下:

则根据状态转移方程,可以得出从顶点 1 到顶点 10 的最小开销为:
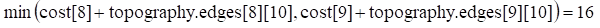
如果我们要找出最短路径,还需要一个一维数组 path[MAXV],用于保存每个顶点的前驱顶点。

找到最短路径的方式为从 path[10] 开始依次访问对应的顶点,访问的次序即为所求的最短路径,直到访问了起点为结束。
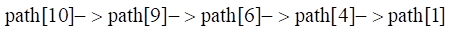
2.3 参考程序 #
首先定义图结构的结构体,使用邻接矩阵来存储:
typedef struct //图的定义
{
int edges[MAXV][MAXV]; //邻接矩阵
int n; //顶点数
} MGraph;
定义求解问题需要的辅助结构:
MGraph topography; //保存城市关系的邻接矩阵
int path[MAXV] = {}; //保存到该顶点的最短路径对应的前驱
int min_cost[MAXV] = {}; //保存到每个顶点的最短路径长
要根据测试样例数据建立多段图的邻接矩阵:
MGraph CreateMGraph(int num) //建图
{
MGraph topography;
int n;
int point1, point2;
int value;
//初始化边为不存在
for(int i = 1; i <= num; i++)
{
for(int j = 1; j <= num; j++)
{
topography.edges[i][j] = 0;
}
}
cout << "请输入边数:";
cin >> n;
for (int i = 0; i < n; i++)
{
cin >> point1 >> point2 >> value;
topography.edges[point1][point2] = value;
}
cout << "\n建立的邻接矩阵为:" << endl;
for(int i = 1; i <= num; i++)
{
for(int j = 1; j <= num; j++)
{
printf("%2d ",topography.edges[i][j]);
}
cout >> endl;
}
cout >> endl;
topography.n = num;
return topography;
}
根据状态转移方程求解问题,最后输出最短路径及其开销:
int main()
{
int cities_num = 0; //城市数量
int a_cost; //当前路径的开销
int pre;
cout << "城市数量为:";
cin >> cities_num;
//建图
topography = CreateMGraph(cities_num);
//初始化路径开销
min_cost[1] = 0;
for(int i = 2; i <= topography.n; i++)
{
min_cost[i] = 99999;
}
//依次计算到达所有点的最短路径
for(int i = 2; i <= cities_num; i++)
{
//遍历之前的所有点,计算到达该点的最短路径
for(int j = 1; j < i; j++)
{
if(topography.edges[j][i] != 0) //若路径存在
{
a_cost = min_cost[j] + topography.edges[j][i];
if(a_cost < min_cost[i]) //更新最短路径长
{
min_cost[i] = a_cost;
path[i] = j; //记录前驱顶点
}
}
}
}
//输出到所有顶点的最短路径
for(int i = 1; i <= cities_num; i++)
{
cout << "到顶点" << i << "的最小开销为:" << min_cost[i] << ",路径:" << i;
pre = i;
while(path[pre])
{
cout << "<-" << path[pre];
pre = path[pre];
}
cout << endl;
}
return 0;
}



