主要内容 #

1. 数字金字塔
2. 求解思路
3. 参考代码

1. 数字金字塔 #

观察下面的数字金字塔。写一个程序查找从最高点到底部任意处结束的路径，使路径经过数字的和最大。每一步可以从当前点走到左下方的点也可以到达右下方的点。

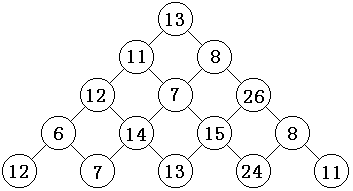
在上面的样例中,从13到8到26到15到24的路径产生了最大的和86。
输入
第一个行包含R(1≤R≤1000)，表示行的数目。
后面每行为这个数字金字塔特定行包含的整数。
所有的被供应的整数是非负的且不大于100。
输出
单独的一行，包含那个可能得到的最大的和。
输入样例

5
13
11 8
12 7  26
6  14 15 8
12 7  13 24 11

输出样例
86

2. 求解思路 #

aij表示数字金字塔上第 𝑖 行从左往右数第 𝑗 个点，则我们的目的就是从 𝑎11 走到第 𝑛 行的 𝑎𝑛𝑖（此处 𝑖 可能是 1∼𝑛 范围内的任何一个点）。很明显这道题目可以用动态规划（DP）求解，但是根据求解的方向不同，对应的状态也不相同。
这里，我们可以以两种思路来解决这个问题：

• 自顶向下（从上往下推）；
• 自底向上（从下往上推）。

下面，我们来分析第一种思路。
1. 确定dp数组的含义
dp[i][j]定义状态表示从a11走到aij的所有路径数字和的最大值。
2. 确定递推公式
当i=1 时（i=1 时只有一个状态 dp[1][1]），dp[1][1]=a11；
当i>1 时,分三种情况：
A.当 j=1 时,dp[i][1]=dp[i-1][j]+ai1（最左边的点只能从右上方走过来）；
B.当 j=i 时,dp[i][1]=dp[i-1][i-1]+aii（最左边的点只能从右上方走过来）；
C.当 1<j<i 时，dp[i][j]=”max{dp[i-1][j-1],” dp[i-1][j]}+aij（中间的点可以选择从左上角或右上角的点走过来，所以选择两者的较大值）。
3. dp数组的初始化
从上面的分析可以知道，dp数组全部初始化为0就可以了。
4. 确定遍历顺序
很显然，我们只需要从上至下外层循环层数，内层从左至右遍历每一层上的数字即可。
令 i=1→n的顺序推导出所有的dp[i][j]则最终的答案就是：
dp[n][1]（从 a11 走到an1的最大数字和）、
dp[n][2]（从 a11 走到an2的最大数字和）、
dp[n][2]（从 a11走到 an3 的最大数字和）、
…… ……
dp[n][n]（从a11走到ann的最大数字和）

3. 参考代码 #

#include<iostream>
using namespace std;
const int maxn = 1010;
int n, a[maxn][maxn], dp[maxn][maxn], ans;
int main()
{
    cin >> n;    
    for (int i = 1; i <= n; i ++)
        for (int j = 1; j <= i; j ++)
            cin >> a[i][j];
    for (int i = 1; i <= n; i ++)
    {
        for (int j = 1; j <= n; j ++)
        {
            if (i == 1) dp[i][j] = a[i][j];
            else if (j == 1) dp[i][j] = dp[i-1][j] + a[i][j];
            else if (j == i) dp[i][j] = dp[i-1][j-1] + a[i][j];
            else dp[i][j] = max(dp[i-1][j-1], dp[i-1][j]) + a[i][j];
        }
    }
    for (int i = 1; i <= n; i ++)
        ans = max(ans, dp[n][i]);
    cout << ans;;
    return 0;
}