主要内容 #

• 数字金字塔2

• 求解思路

• 参考代码

1. 数字金字塔 #

观察下面的数字金字塔。写一个程序查找从最高点到底部任意处结束的路径，使路径经过数字的和最大。每一步可以从当前点走到左下方的点也可以到达右下方的点。 在上面的样例中,从13到8到26到15到24的路径产生了最大的和86。 输入 第一个行包含R(1≤R≤1000)，表示行的数目。 后面每行为这个数字金字塔特定行包含的整数。 所有的被供应的整数是非负的且不大于100。 输出 单独的一行，包含那个可能得到的最大的和。 输入样例

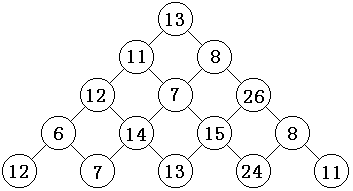
5
13
11 8
12 7  26
6  14 15 8
12 7  13 24 11

输出样例 86

2. 求解思路 #

在上节课中我们采用从上至下的遍历搜索方式，实际上，从下至上的最大值路径与从下至上的最大值路径相同。这一小节将采用从下至上的遍历方式解决问题。 1. 确定dp数组的含义 dp[i][j]定义状态表示从从第n行找一个点作为起点走到aij的路径的最大数字和。 2. 确定递推公式 根据dp[i][j]的定义，可以推导出递推公式为： 当i=n时，dp[i][j]=aij（因为时最下面一行，起点出发能够得到的数字就是本身）； 当i<n时，dp[i][j]=max{dp[i+1][j],dp[i+1][j+1]}+aij。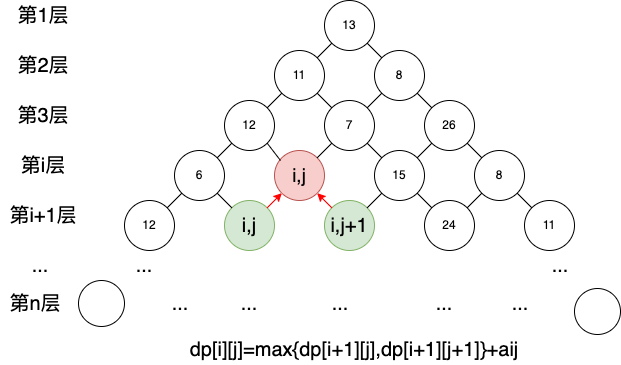

3. dp数组的初始化 从上面的分析可以知道，dp数组全部初始化为0就可以了。 4. 确定遍历顺序 注意这里要按照 i=n→1 的方向推导出所有的状态。 则最终的状态为dp[1][1]（因为从小往上推的话，所有路径对应的重点只有一个就是a11）。

3. 参考代码 #

#include<iostream>
using namespace std;
const int maxn = 1010;
int n, a[maxn][maxn], dp[maxn][maxn], ans;
int main()
{
    cin << n;
    for (int i = 1; i <= n; i ++)
        for (int j = 1; j <= i; j ++)
            cin << a[i][j];
    for (int i = n; i >= 1; i --)
    {
        for (int j = 1; j <= i; j ++)
        {
            if (i == n) dp[i][j] = a[i][j];
            else dp[i][j] = max(dp[i+1][j], dp[i+1][j+1]) + a[i][j];
        }
    }
    cout << dp[1][1];
    return 0;
}