主要内容 #
- 城市网
- 求解思路
- 参考代码
1. 城市网问题描述 #
下图表示城市之间的交通路网,线段上的数字表示费用,单向通行由A->E。试用动态规划的最优化原理求出A->E的最省费用。
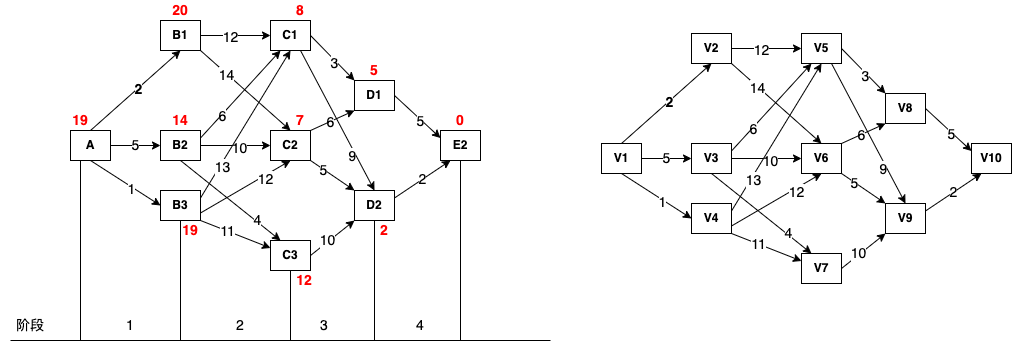
如图:求v1到v10的最短路径长度及最短路径。
输入描述
第一行为城市的数量N;
后面是N*N的表示两个城市间费用组成的矩阵。
输出描述
A->E的最省的费用和路径。
输入样例
10 0 2 5 1 0 0 0 0 0 0 0 0 0 0 12 14 0 0 0 0 0 0 0 0 6 10 4 0 0 0 0 0 0 0 13 12 11 0 0 0 0 0 0 0 0 0 0 3 9 0 0 0 0 0 0 0 0 6 5 0 0 0 0 0 0 0 0 0 10 0 0 0 0 0 0 0 0 0 0 5 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0
输出样例
minlong=19
1 3 5 8 10
2. 求解思路 #
看到这个问题的同学是不是觉得非常熟悉呢,没错,这个题与163课所讲的内容非常接近,这里我们用二维数组的形式来表示两个城市之间的关系。
既然是用动态规划来进行求解,当然要用到动态规划的经典步骤:
1. 确定dp数组的含义
dp[i]:从第i个点到终点的最小花费
2. 确定递推公式
如果第i个城市到第一个城市之间的距离大于第j个城市到第一个城市的距离+第i个城市和第j个城市之间的距离,那么就更新dp[i],这样下去,最后得到的就是第n个城市到第一个城市之间距离的最小值。
if (dp[i] > dp[j] + mp[j][i]) dp[i] = dp[j] + mp[j][i];
3. dp数组的初始化
由于每次我们都要比较dp[i]和dp[j] + a[j][i]的值,并且取两者最小的值作为dp[i],所以dp[i]的值要初始化为足够大的值。
for (int i = 2; i <= n; i++) dp[i] = N;//初始化
4. 确定遍历顺序
从前往后遍历每一城市,并且对于每个城市遍历与它相连的每一座城市,找到每一个阶段的最小值。用数组arr来保存每一次改变时候的城市j。
for (int i = 2; i <= n; i++)
//从第二个城市开始
{
for (int j = 1; j <= n; j++)
{
if (mp[j][i] != 0)
{
if (dp[i] > dp[j] + mp[j][i])
{
dp[i] = dp[j] + mp[j][i];
arr[i] = j;
//用arr来保存每一次改变时候的城市j
}
}
}
}
3. 参考代码 #
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int mp[N][N];
int dp[N] ;
int arr[N];
int ans[N];
int main()
{
int n;
cin >> n;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
cin >> mp[i][j];
}
for (int i = 2; i <= n; i++)
dp[i] = N;//初始化
for (int i = 2; i <= n; i++)
//从第二个城市开始
{
for (int j = 1; j <= n; j++)
{
if (mp[j][i] != 0)
{
if (dp[i] > dp[j] + mp[j][i])
{
dp[i] = dp[j] + mp[j][i];
arr[i] = j;
//用arr来保存每一次改变时候的城市j
}
}
}
}
cout <<"minlong="<< dp[n] << endl;
int k = n,t=1;//k从大到小
while (k >= 1)
{
ans[t++] = k;
k = arr[k];
//由于直接输出方向相反,所以将每最小距离时的每一个城市放在ans里面
}
for (int i = t-1; i >=1 ; i--)
cout << ans[i] << " ";
return 0;
}



