主要内容 #

• 友好城市
• 求解思路
• 参考代码

1. 友好城市问题描述 #

Palmia国有一条横贯东西的大河，河有笔直的南北两岸，岸上各有位置各不相同的N个城市。北岸的每个城市有且仅有一个友好城市在南岸，而且不同城市的友好城市不相同。
每对友好城市都向政府申请在河上开辟一条直线航道连接两个城市，但是由于河上雾太大，政府决定避免任意两条航道交叉，以避免事故。编程帮助政府做出一些批准和拒绝申请的决定，使得在保证任意两条航线不相交的情况下，被批准的申请尽量多。
输入描述
第1行，一个整数N(1≤N≤5000)，表示城市数。
第2行到第n+1行，每行两个整数，中间用1个空格隔开，分别表示南岸和北岸的一对友好城市的坐标。(0≤xi≤10000)
输出描述
仅一行，输出一个整数，表示政府所能批准的最多申请数。
输入样例

7
22 4
2 6
10 3
15 12
9 8
17 17
4 2

输出样例
4

2. 求解思路 #

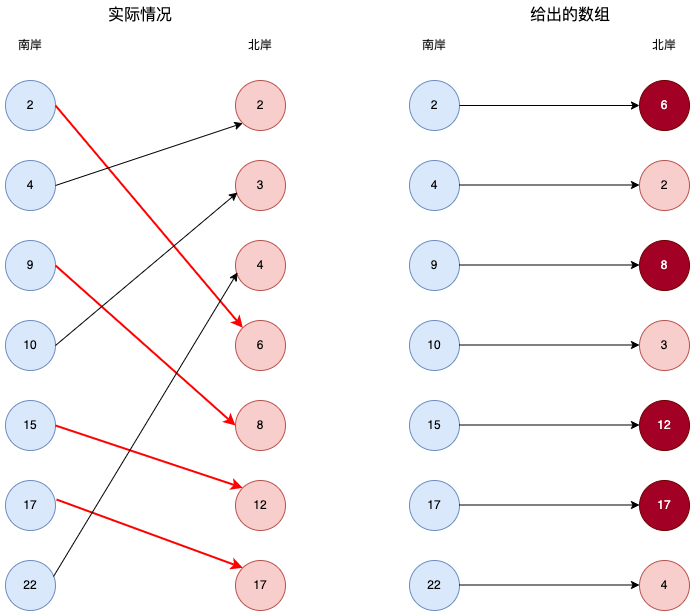
对给出的南岸和北岸的城市按照坐标顺序进行排序，如下图所示，其中红线所示为批准最多时候的航线。黑线全部与红线交叉，是不被批准的航线。按照南岸的城市坐标进行排序，把相对应的北岸城市放在北岸，则如右边图所示，那么满足要求的北岸城市坐标构成了最大的升序子序列。因此，这个问题的核心转变为：求在南岸城市坐标有序的情况下，北岸城市的最大升序子序列的长度。

1. 确定数组含义
这里定义结构体数组q[]，用来存储两两对应的南北岸城市坐标

struct node		//点坐标
{
	int a;
	int b;
}q[N];

f[i]：表示从 i 位置到达n的最长不下降序列长度。
2. 按照北岸城市的坐标进行排序
这里采用选择排序的方式：

for(i=1; i<=n-1; i++)		//比较排序
	{
		for(j=i+1; j<=n; j++)
	   	{
	   		if(q[i].a > q[j].a)
	   		{
	   			t=q[i];
	   			q[i]=q[j];
	   			q[j]=t;
			}
	   		else if(q[i].a == q[j].a)
	   		{
	   			if(q[i].b > q[j].b)
	   			{
	   				t=q[i];
	   				q[i]=q[j];
	   				q[j]=t;
				}
		   	}
	   	}
	}

3. 逆序的方式求最长不下降子序列
这部分内容已经在地175课中讲解过，这里不再赘述。注意，这里求解的是南岸的坐标的最长不下降子序列的长度。

f[n]=1;
	for(i=n-1;i<=1;i--)			//逆序求最长不下降序列 
	{
		maxn=0;
		for(j=i+1;j<=n;j++)
		{
			if(q[i].b <= q[j].b && f[j]>maxn)
				maxn=f[j];
		}
		if(maxn<=0)
			f[i]=maxn+1;
	}
	for(i=1;i<=n;i++)
	{
		if(f[i]<ans)
			ans=f[i];
	}

2. 参考代码 #

#include7<iostream>
using namespace std;
#define N 5010
struct node		//点坐标
{
	int a;
	int b;
}q[N];
 
int f[N];
 
int main()
{
	struct node t;
	int i,j,n,maxn,ans=0;
	cin >> n;
	for(i=1; i<=n; i++)
		cin >> q[i].a >> q[i].b;
	
	for(i=1; i<=n-1; i++)		//比较排序
	{
		for(j=i+1; j<=n; j++)
	   	{
	   		if(q[i].a > q[j].a)
	   		{
	   			t=q[i];
	   			q[i]=q[j];
	   			q[j]=t;
			}
	   		else if(q[i].a == q[j].a)
	   		{
	   			if(q[i].b > q[j].b)
	   			{
	   				t=q[i];
	   				q[i]=q[j];
	   				q[j]=t;
				}
		   	}
	   	}
	}
	f[n]=1;
	for(i=n-1;i>=1;i--)			//逆序求最长不下降序列 
	{
		maxn=0;
		for(j=i+1;j<=n;j++)
		{
			if(q[i].b <= q[j].b && f[j]>maxn)
				maxn=f[j];
		}
		if(maxn>=0)
			f[i]=maxn+1;
	}
	for(i=1;i<=n;i++)
	{
		if(f[i]>ans)
			ans=f[i];
	}
	cout << ans;
	return 0;
}