主要内容 #

• 合唱队形
• 求解思路
• 参考代码

1. 合唱队形问题描述 #

N位同学站成一排，音乐老师要请其中的(N−K)位同学出列，使得剩下的KK位同学排成合唱队形。
合唱队形是指这样的一种队形：设K位同学从左到右依次编号为1,2,…,K，他们的身高分别为T1,T2,…,TK，则他们的身高满足T1<T2<…<Ti,Ti>Ti+1>…>TK(1≤i≤K)。
你的任务是，已知所有N位同学的身高，计算最少需要几位同学出列，可以使得剩下的同学排成合唱队形。
输入描述
输入的第一行是一个整数N（2≤N≤100），表示同学的总数。第二行有n个整数，用空格分隔，第i个整数Ti（130≤Ti≤230）是第i位同学的身高（厘米）。
输出描述
输出包括一行，这一行只包含一个整数，就是最少需要几位同学出列。
输入样例

8
186 186 150 200 160 130 197 220

输出样例
4

2.求解思路 #

1. 问题分析
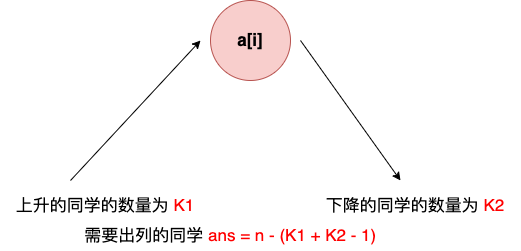
根据题目要求，合唱队形就是以第i个同学作为基准，在他左边的同学依次上升，在他右边的同学依次下降，这样就构成一个山形，那么第i个作为基准的同学的身高最高，如下图所示。
题目中要求计算出最小的出列同学数量，换句话说，就是要求尽可能多的同学留在队内。也就是以第i个同学作为基准，左边的上升子序列长度加上右边的下降子序列长度的结果最大。这个题目又回到了求解最长上升或者下降子序列的问题上来。

2. 举例说明
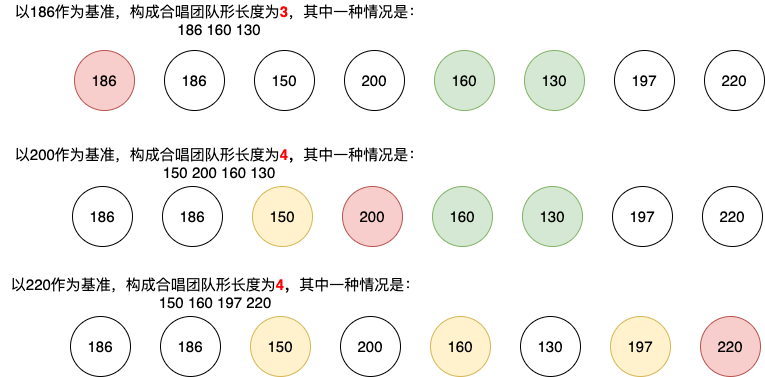
以题目中所给的样例作为例子进行说明：

3. 变量解释
a为身高序列，其中 a[i]为同学 i 的身高。
b为由左而右身高递增的人数序列，其中 b[i]为同学 1…同学 i 间（包括同学 i）身高满足递增顺序的最多人数。显然b[i] = max { b[j] | 同学 j 的身高 < 同学 i 的身高 +1，1<=j<=i-1 }。

c为由右而左身高递增的人数序列，其中 c[i]为同学 n…同学 i 间（包括同学 i）身高满足递增顺序的最多人数。显然 c[i] = max { c[j] | 同学 j 的身高 < 同学 i 的身高 +1，i+1<=j<=n }。

显然，合唱队的人数为max { b[i]+c[i] } -1（公式中的同学 i 被重复计算，因此减1）。

3.参考程序 #

#include <iostream>
using namespace std;
#define N 110
int a[N];
int b[N];  // 以第i位同学为终点的最长上升序列的长度 
int c[N];  // 以第i位同学为起点的最长下降序列的长度
int ans;
int main()
{
	int i,j,n;
	int maxn;
	cin >> n;
	for(i=1;i<=n;i++)
		cin >> a[i];

	// 以第i位同学为终点的最长上升序列
	b[1]=1;
	for(i=2;i<=n;i++)
	{
		maxn=0;
		for(j=1;j<i;j++)
		{
			if(a[i]>a[j])
			{
				if(b[j]>maxn)
					maxn=b[j];
			}
		}
		b[i]=maxn+1;
	}

	// 以第i位同学为起点的最长下降序列
	c[n]=1;
	for(i=n-1;i>=1;i--)
	{
		maxn=0;
		for(j=i+1;j<=n;j++)
		{
			if(a[i]>a[j])
			{
				if(c[j]>maxn)
					maxn=c[j];
			}
		}
		c[i]=maxn+1;
	}

	for(i=1;i<=n;i++)
		if(b[i]+c[i]>ans)
			ans=b[i]+c[i];
	cout << n-(ans-1) << endl;;
	return 0;
}