跳至正文
View Categories

1 min read

主要内容 #

  • 最长公共子序列
  • 求解思路
  • 参考代码

1. 最长公共子序列问题描述 #

一个给定序列的子序列是在该序列中删去若干元素后得到的序列。确切地说，若给定序列X=<x1,x2,…,xm>，则另一序列z＝<z1，z2，…，zk>是x的子序列是指存在一个严格递增的下标序列<i1,i2,…,ik>,使得对于所有j=1,2,…,k有：Xij=Zj

例如，序列Z=<b,c,d,b>是序列X=<a,b,c,b,d,a,b>的子序列,相应的递增下标序列为<2,3,5,7>。给定两个序列X和Y，当另一序列Z既是X的子序列又是Y的子序列时，称Z是序列X和Y的公共子序列。例如，若X＝<a,b,c,b,d,a,b>和Y＝<b,d,c,a,b,a>，则序列<b,c,a>是X和Y的一个公共子序列,序列 <b,c,b,a>也是X和Y的一个公共子序列。而且，后者是X和Y的一个最长公共子序列．因为X和Y没有长度大于4的公共子序列。

给定两个序列X＝<x1，x2，…，xm>和Y=<y1,y2…．yn>．要求找出X和Y的一个最长公共子序列。
输入描述
共有两行。每行为一个由大写字母构成的长度不超过1000的字符串，表示序列X和Y。
输出描述
第一行为一个非负整数。表示所求得的最长公共子序列的长度。若不存在公共子序列．则输出文件仅有一行输出一个整数0。
输入样例

ABCBDAB
BDCABA

输出样例
4
提示
最长公共子串（Longest Common Substirng）和最长公共子序列（Longest Common Subsequence，LCS）的区别为：子串是串的一个连续的部分，子序列则是从不改变序列的顺序，而从序列中去掉任意的元素而获得新的序列；也就是说，子串中字符的位置必须是连续的，子序列则可以不必连续。字符串长度小于等于1000。

2. 求解思路 #

设f[i][j]表示序列a[1…i]和b[1…j]的最长公共子序列长度，令a[]数组为ADABEC，b[]数组为DBDCA，考查末尾元素a[i]与b[j]是否在公共子序列中：
（1）若a[i]=b[j]，则a[i]与b[j]在公共子序列中。

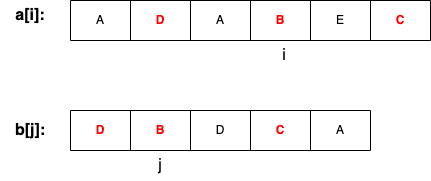
a[1…i-1, i] → a[1…i-1] + a[i]；
b[1…j-1, j] → b[1…j-1] + b[j]。
所以， f[i][j] = f[i-1][j-1] + 1。
（2）若a[i]≠b[j]，且a[i]不在公共子序列中，则可以去掉a[i]。

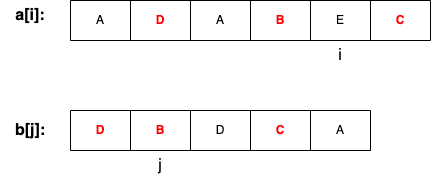
a[1…i-1, i] → a[1…i-1]；
b[1…j-1, j] → b[1…j-1, j] 。
所以， f[i][j] = f[i-1][j]。
（3）若a[i]≠b[j]，且b[i]不在公共子序列中，则可以去掉b[i]。

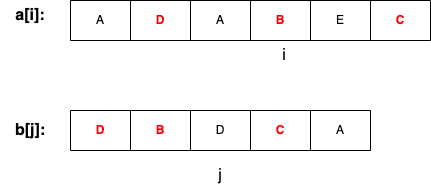
a[1…i-1, i] → a[1…i-1, i] ；
b[1…j-1, j] → b[1…j-1] 。
所以， f[i][j] = f[i][j-1]。
1. 确定dp数组的含义
为算法上的需要，定义两个字符数组，用于存储两个字符串，一个二维数组，用于求解最长公共子序列。
（1）a[i]：存储字符串。
（2）b[j]：存储字符串。
（3）f[i][j]：表示前缀子串a[1…i]与b[1…j]的“最长公共子序列”的长度。
2. 确定递推公式
f[i][j]的值从哪来？当a[i]=b[j]时，从f[i-1][j-1]而来，当a[i]≠b[j]时，从f[i-1][j] 或 f[i][j-1]而来
（1）若a[i]=b[j]：f[i][j] = f[i-1][j-1] + 1。
（2）若a[i]≠b[j]：f[i][j] = max(f[i][j-1], f[i-1][j])。
3. dp数组进行初始化
边界：f[i][0] = f[0][j] = 0，目标：f[n][m]。
4. 循环顺序
从递推公式可知，f[i][j]是由f[i-1][j-1]、f[i][j-1]、f[i-1][j]推导而来，也就是从小的序列推导至大的序列，所以循环也是从小至大。

for(i=1;i<=len_s;i++)
{
    for(j=1;j<=len_t;j++)
    {
        if(s[i-1]==t[j-1])
		f[i][j]=f[i-1][j-1]+1;
	else
		f[i][j]=max(f[i-1][j],f[i][j-1]);
    }
 }

3.参考程序 #

#include <iostream>
#include <string.h>
using namespace std;
#define MAXN 1010
 
int f[MAXN][MAXN];      //dp数组
char s[MAXN],t[MAXN];   //用来存储两个字符串
 
int max(int x,int y)
{
	return x > y ? x : y;
}
int main()
{
	int i,j;
	int len_s,len_t;       //用来存储两个字符串的长度
	cin >> s >> t;
	
	len_s=strlen(s);
	len_t=strlen(t);
	
	for(i=1;i<=len_s;i++)
	{
		for(j=1;j<=len_t;j++)
		{
			if(s[i-1]==t[j-1])
				f[i][j]=f[i-1][j-1]+1;
			else
				f[i][j]=max(f[i-1][j],f[i][j-1]);
		}
	}
	cout << f[len_s][len_t];
	return 0;
}
What are your Feelings