主要内容 #

1. 双亲表示法
2. 孩子表示法
3. 孩子兄弟表示法

1. 双亲表示法 #

采用的一组连续的存储空间来存储每个节点。根节点没有双亲，所以其在数组中存储的值为-1。其余的节点，只需要存储其父节点对应的数组下标即可。如下图所示：

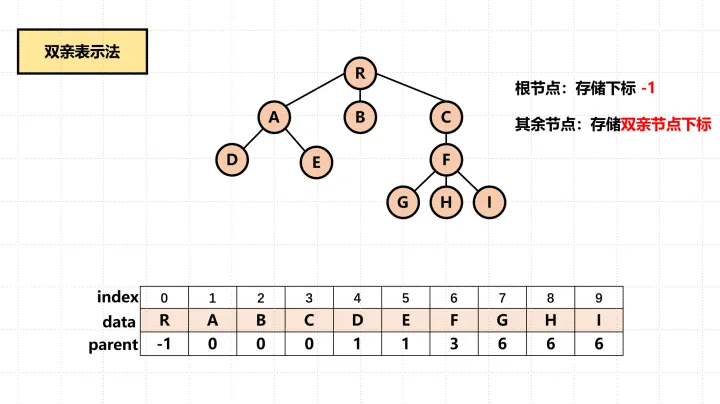
优缺点：利用了树中除根节点外的每个节点都有唯一的父亲节点这个性质，很容易找到树的根，但找到孩子节点可以遍历整个线性表。

const int m = 10;   //树的节点数
struct node{
    int data, parent; //数据域，指针域
};
node tree[m];

2. 孩子表示法 #

将每个节点的孩子节点都用单链表连接起来形成一个线性结构，n个节点具有n个孩子链表。

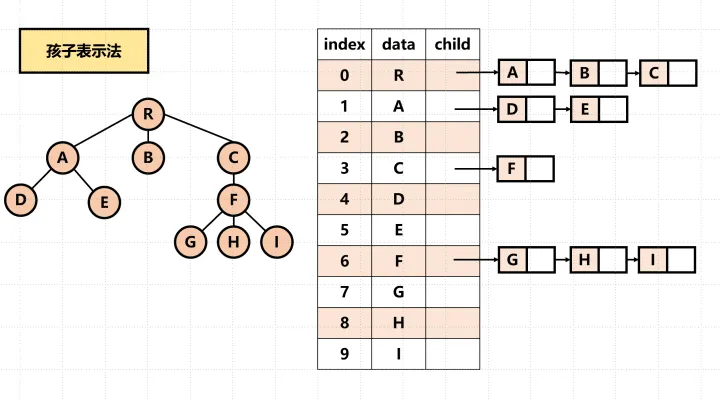
还可以这样表示：

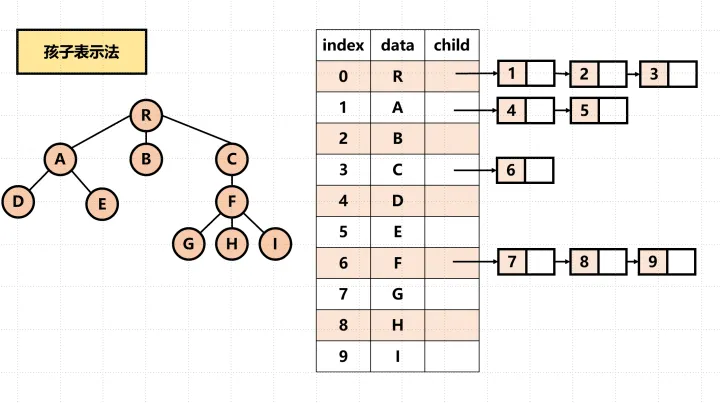
优缺点：只能从根节点遍历到子节点，不能从某个子节点返回到它的父节点。

const int m = 10;   //树的度
typedef struct node;
typedef node *tree;
struct node{
    char data;     //数据域
    tree child[m]; //指针域，指向若干孩子节点
};
tree t;

3.孩子双兄弟表示法 #

以二叉链表作为树的存储结构，又称二叉树表示法。其中孩子指针域，表示指向当前结点的第一个孩子结点，兄弟结点表示指向当前结点的下一个兄弟结点。

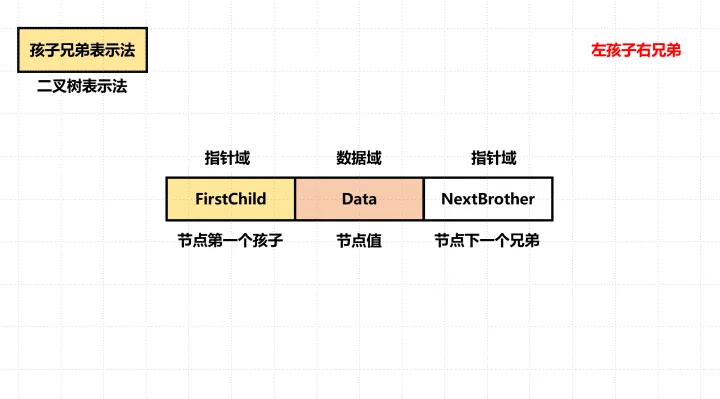
使用孩子兄弟表示法需要将树转换为二叉树。
转化前：

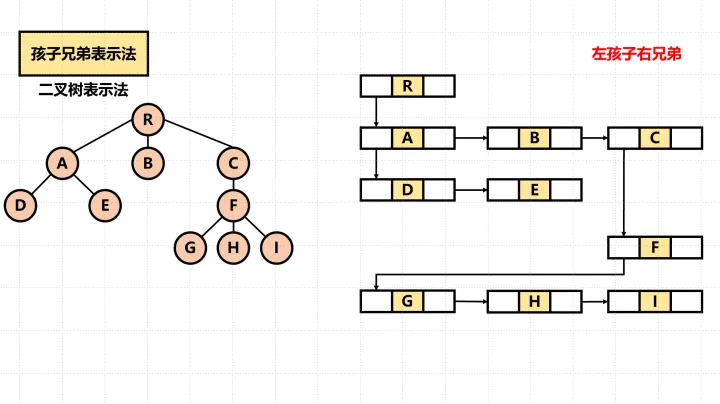
转化后：

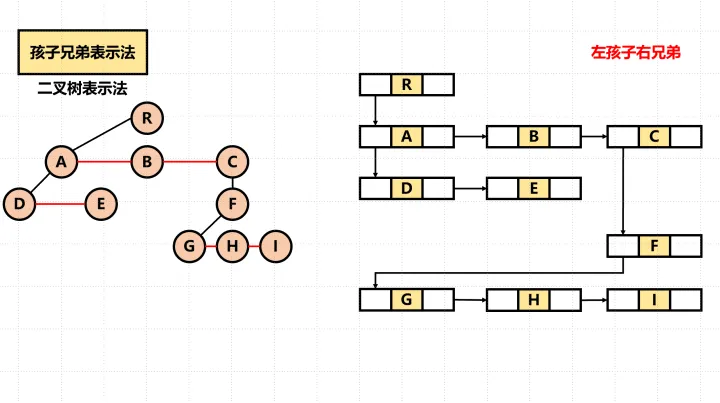
typedef struct node;
typedef node *tree;
struct node{
    char data;     //数据域
    tree firstchild, next; //指针域，指向第一个孩子和下一个兄弟节点
};
tree t;

总结
树的三种表示方法中，双亲表示法和孩子表示法在实际算法中的应用场景正好相反：双亲表示法应用于解决查找某结点的父结点，而孩子表示法应用于查找某结点的孩子结点。
孩子兄弟表示法可以将普通树转化成二叉树存储，在实际操作中，可以应用二叉树的性质来解决普通树或者森林的问题。