跳至正文
View Categories

1 min read

主要内容 #

  1. 遍历的种类
  2. 前序遍历
  3. 中序遍历
  4. 后续遍历
  5. 层序遍历

1.遍历的种类 #

树的遍历是一种图的遍历，指的是按照某种规则，不重复地访问某种树的所有节点的过程。具体的访问操作可能是检查节点的值、更新节点的值等。不同的遍历方式，其访问节点的顺序是不一样的。以下虽然描述的是二叉树的遍历算法，但它们也适用于其他树形结构。

树结构有多种不同的遍历方式，从二叉树的根节点出发，节点的遍历分为三个主要步骤：对当前节点进行操作（称为“访问”节点）、遍历左边子节点、遍历右边子节点。这三个步骤的先后顺序也是不同遍历方式的根本区别。

遍历方式的命名，源于其访问节点的顺序。最简单的划分：是深度优先（先访问子节点，再访问父节点，最后是第二个子节点）和广度优先（先访问第一个子节点，再访问第二个子节点，最后访问父节点。 深度优先可进一步按照根节点相对于左右子节点的访问先后来划分。

如果把左节点和右节点的位置固定不动，那么根节点放在左节点的左边，称为前序（pre-order）、根节点放在左节点和右节点的中间，称为中序（in-order）、根节点放在右节点的右边，称为后序（post-order）。对广度优先而言，遍历没有前序中序后序之分：给定一组已排序的子节点，其“广度优先”的遍历只有一种唯一的结果。

2. 前序遍历 #

前序遍历（Pre-Order Traversal）是依序以根节点、左节点、右节点为顺序遍历的方式。如下图所示：

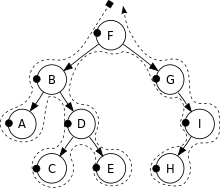
深度优先遍历（前序遍历）的结果为：F, B, A, D, C, E, G, I, H。
采用递归方式的算法实现为：

void pre_order_traversal(TreeNode *root) {
    // Do Something with root
    if (root->lchild != NULL) //若其左子树为空
        pre_order_traversal(root->lchild);
    if (root->rchild != NULL) //另一侧的子树也做相同事
        pre_order_traversal(root->rchild);
}

3. 中序遍历 #

中序遍历（In-Order Traversal）是依序以左节点、根节点、右节点为顺序遍历的方式。

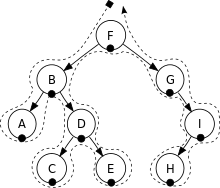
深度优先遍历（中序遍历）的结果为：A, B, C, D, E, F, G, H, I。
采用递归方式的算法实现为：

void in_order_traversal(TreeNode *root) {
    if (root->lchild != NULL) //若其中一侧的子树非空则读取取其子树
        in_order_traversal(root->lchild);
    // Do Something with root
    if (root->rchild != NULL) //另一侧的子树也做相同事
        in_order_traversal(root->rchild);
}

4. 后序遍历 #

后序遍历（Post-Order Traversal）是依序以左节点、右节点、根节点为顺序遍历的方式。

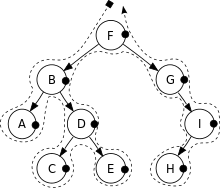
深度优先搜索（后序遍历）的结果为：A, C, E, D, B, H, I, G, F。
采用递归方式的算法实现为：

void post_order_traversal(TreeNode *root) {
    if (root->lchild != NULL) //若其中一侧的子树非空则读取取其子树
        post_order_traversal(root->lchild);
    if (root->rchild != NULL) //另一侧的子树也做相同事
        post_order_traversal(root->rchild);
    // Do Something with root
}

5. 层序遍历 #

和深度优先遍历不同，广度优先遍历会先访问离根节点最近的节点。二叉树的广度优先遍历又称按层次遍历。

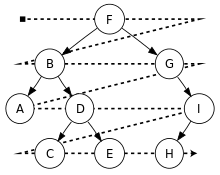
广度优先遍历 – 层次遍历的结果是：F, B, G, A, D, I, C, E, H。
算法借助队列实现：

void level(TreeNode *node)
{
  Queue *queue = initQueue();
  enQueue(queue, node);

  while (!isQueueEmpty(queue))
  {
    TreeNode *curr = deQueue(queue); //出队操作

    // Do Something with curr

    if (curr->lchild != NULL)
      enQueue(queue, curr->lchild); //左子树入队
    if (curr->rchild != NULL)
      enQueue(queue, curr->rchild); //右子树入队
  }
}
What are your Feelings