主要内容 #
- 二叉树的基本概念
- 二叉树的性质
1.二叉树的基本概念 #
二叉树(英语:Binary tree,简写成BT)是每个节点最多只有两个分支(即不存在分支度大于2的节点)的树结构[1]。通常分支被称作“左子树”或“右子树”。二元树的分支具有左右次序,不能随意颠倒。二叉树有5种基本的形态:
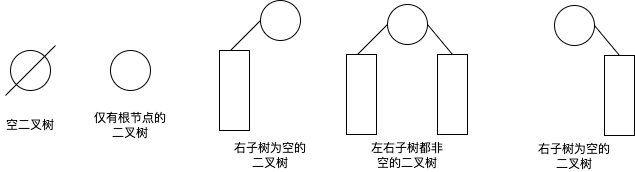
前面引入的树的术语也基本适用于二叉树,但二叉树也有很多不同,如:首先二叉树的每个节点至多只能有两个子节点,二叉树可以为空,二叉树一定是有序的,通过它的左右子树的关系体现出来。
2.二叉树的性质 #
2.1 性质1 #
在二叉树的第i层上最多有2^(i-1)个节点(i>=1)。
证明:很简单,用归纳法:当i=1时,2^(i-1)=1显然成立;现在假设第i-1层时命题成立,即i-1层上有最多2^(i-2)个节点。由于二叉树的每个节点的度最多为2,故在第i层上的最大节点数为第i-1层的2倍,即2*2^(i-2)=2^(i-1)。
2.2 性质2 #
深度为k的二叉树至多有2^k-1个节点(k>=1)。
证明:在具有相同深度的二叉树中,仅当每一层都含有最大的节点数时,其树中节点数最多。因此利用性质1可得,深度为k的二叉树的节点数至多为:
2^0+2^1+···+2^(k-1)=2^k-1
故命题正确。
特别:一棵深度为k且有2^k-1个节点的二叉树称为满二叉树。如图1为深度为4的满二叉树,这种树的特点是每层上的节点数都是最大节点数。
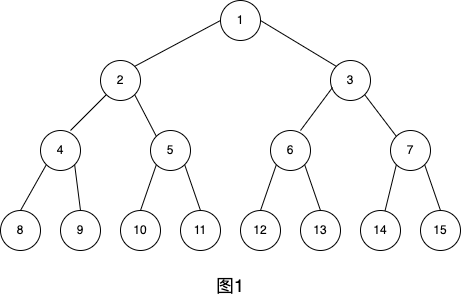
可以对满二叉树的节点进行连续编号,约定编号从根节点起,自上而下,从左到右,由此引出完全二叉树的定义,深度为k,有n个节点的二叉树,当且仅当每个节点都与深度为k的满二叉树中编号从1到n的节点一一对应时称为完全二叉树。
或者说,在一颗二叉树中,若除最后一层外的其余层都是满的,并且最后一层要么是满的,要么在右边缺少连续若干节点,则此二叉树为完全二叉树。
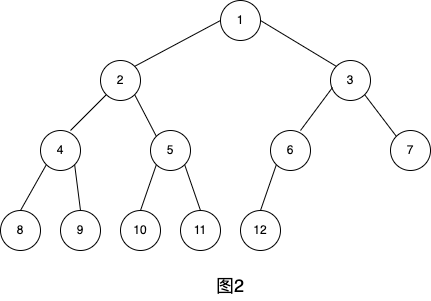
图2就是一棵深度为4的,节点数为12的完全二叉树。
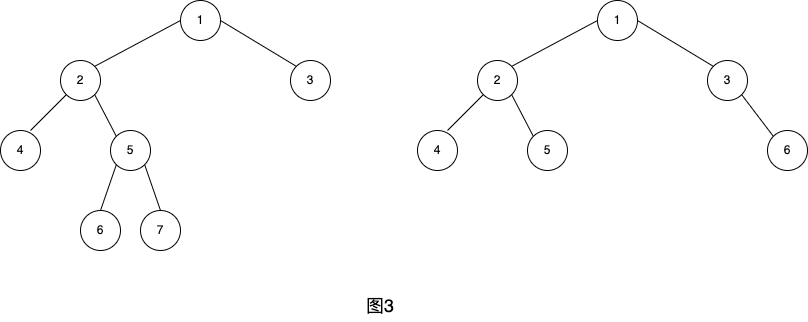
它有如下特征:叶子节点只能在层次最大的两层中出现;对任一节点,若其右分枝下的子孙的最大层次为m则在其左分枝下的子孙的最大层次必为m或m+1。图3中的两个树不是完全二叉树,请大家思考为什么?
2.3 性质3 #
对于任意一棵二叉树,如果其叶子节点数为n0,度为2的节点数为n2,则一定满足:n0=n2+1。
证明:因为二叉树中所有的节点的度均不大于2,所以节点总数(记为n)应等于0度的节点数n0、1度的节点数n1、2度的节点数n2之和:
式子1:n=n0+n1+n2
另一方面,1度的节点只有一个孩子,2度的节点有2个孩子,故二叉树中孩子节点总数是:n1+2*n2
树中仅有根节点不是任何节点的孩子,故二叉树中的节点总数又可表示为:
式子2;n=n1+2*n2+1
由式子1和2得到:
n0=n2+1
2.4 性质4 #
具有n个节点的完全二叉树的深度为:k=floor(logn)+1。
证明:假设深度为k,根据完全二叉树的定义,前面k-1层一定是满的,所以n>2^(k-1)-1。但n又满足n<=2^k-1,所以,2^(k-1)-1<n<=2^k-1,变换一下为:2^(k-1)-1<=n<2^k-1。以2为底取对数可以得到:k-1<logn<k,所以k=floor(logn)+1。
2.5 性质5 #
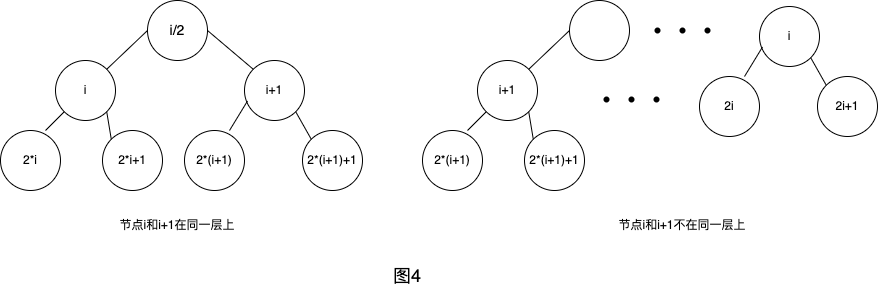
对于一棵n个节点的完全二叉树,对于任一节点(编号为i)有:
- 如果i=1,则节点为根,无父节点;如果i>1,则其父节点的编号为i/2。如果2*i>n,则节点i无左孩子(当然也无右孩子了),左孩子的编号为2*i。
- 如果2*i+1>n,则节点i无右孩子,否则,右孩子的编号为2*i+1。
我们只需验证一下即可,如图4所示: