跳至正文
View Categories

< 1 min read

主要内容 #

  1. 顺序存储结构
  2. 链式存储结构

二叉树是非线性结构，其存储结构可以分为两种，即顺序存储结构和链式存储结构。

1.顺序存储结构 #

二叉树的顺序存储，指的是使用顺序表（数组）存储二叉树。
需要注意的是，顺序存储只适用于完全二叉树。对于普通的二叉树，必须先将其转化为完全二叉树，才能存储到顺序表中。满二叉树也是完全二叉树，可以直接用顺序表存储。
一棵普通二叉树转化为完全二叉树的方法很简单，只需要给二叉树额外添加一些结点，就可以把它”拼凑”成完全二叉树。如图 1 所示：

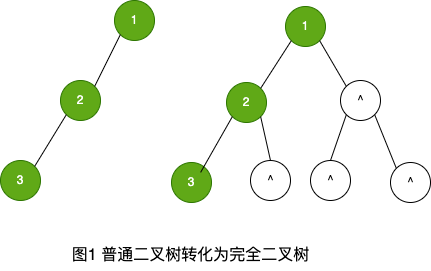
图 1 左侧是普通二叉树，右侧是转化后的完全（满）二叉树。解决了二叉树的转化问题，接下来学习如何顺序存储完全（满）二叉树。
所谓顺序存储完全二叉树，就是从树的根结点开始，按照层次将树中的结点逐个存储到数组中。

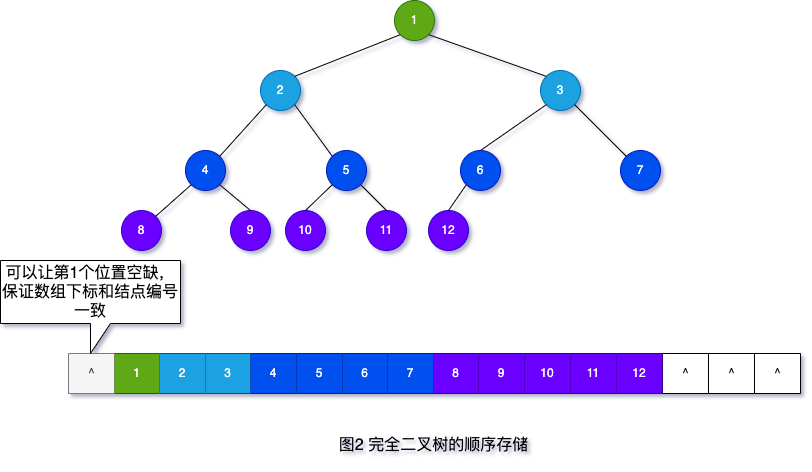
存储由普通二叉树转化来的完全二叉树也是如此，比如将图 1 中的普通二叉树存储到顺序表中，树中结点的存储状态如图 3 所示：

几个重要点:
1. i的左孩子——2i
2.  i的右孩子——2i+1
3. i的父节点——i/2向下取整
若完全二叉树中共有n个结点，则:
1. 判断i是否有左孩子——2i<=n
2. 判断i是否有右孩子——2i+1<=n
3. 判断i是否是叶子/分支结点——i>n/2向下取整
二叉树的顺序存储结构用 C 语言表示为：

#define MaxSize 100
struct TreeNode{
    ElemType value;  // 结点中的数据元素
    bool isEmpty;  // 结点是否为空
};
//定义一个长度为MaxSize的数组t，按照从上至下、从左至右的顺序依次存储完全二叉树的各个结点。
TreeNode t[MaxSize];

// 初始化时所有结点标记为空
for(int i=0;i<MaxSize;i++){
    t[i].isEmpty=true;
}

2.链式存储结构 #

介绍了二叉树的顺序存储结构，通过学习你会发现，其实二叉树并不适合用顺序表存储，因为并不是每个二叉树都是完全二叉树，普通二叉树使用顺序表存储或多或多会存在内存浪费的情况。

接下来我们学习二叉树的链式存储结构。

二叉树的链式存储结构是指用链表来表示一棵二叉树，即用链来指示元素的逻辑关系。二叉树的每个结点最多有两个孩子，因此，每个结点除了存储自身的数据外，还应设置两个指针分别指向左、右孩子结点。结点结构如下图所示：

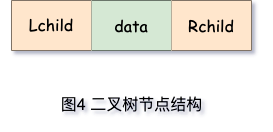
所谓二叉树的链式存储，其实就是用链表存储二叉树，具体的存储方案是：从树的根节点开始，将各个节点及其左右孩子使用链表存储。

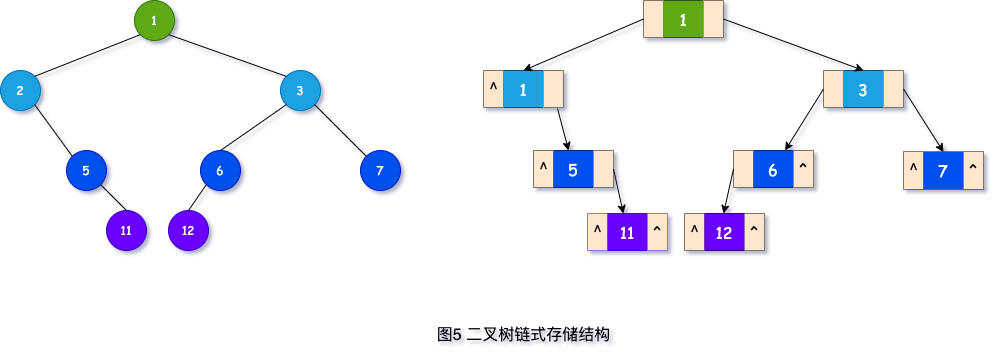
如图5所示，左边是一个普通的二叉树，右边为它的链式存储结构。
二叉树的链式存储结构用 C 语言表示为：

// 定义一棵空树
BiTNode root = NULL;
// 插入根结点
root = (BiTree)malloc(sizeof(BiTNode));
root->data={1};
root->lchild=NULL;
root->rchild=NULL;
// 插入新结点
BiTNode *p=(BiTNode *)malloc(sizeof(BiTNode));
p->data={2};
p->lchild=NULL;
p->rchild=NULL;
root->lchild=p;  // 作为根结点的左孩子
What are your Feelings