主要内容 #

1. 建立一棵二叉树
2. 删除一棵二叉树

1. 建立一棵二叉树 #

定义二叉树的节点：

#include<iostream>
#include<cstdlib>
#include<cstdio>
typedef struct node;
typedef node *tree;
struct node{
    char data;
    tree lchild, rchild;
};

采用递归的方式建立一棵二叉树：

void pre_crt(tree &bt){
    char ch;
    ch = getchar(); //bt 为指向根节点的指针，'¥'表示为空
    if(ch != '¥'){
        bt = new node;  //建立根节点
        bt -> data = ch;
        pre_crt(bt -> lchild);  //建立左子树
        pre_crt(bt -> rchild);  //建立右子树
    }
    else bt = NULL;  //是一棵空树
}

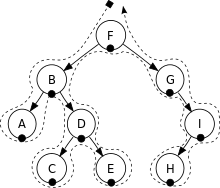
值得注意的是，这种建立树的方式，需要按照前序遍历的顺序输入，并且在遇到左子树或者右子树为空时，需要输入’¥’字符来终止递归，如要产生下面的一棵二叉树，则输入的顺序为：F, B, A,¥,¥, D, C, ¥,¥,E,¥,¥,G,¥,I, H,¥,¥,¥.

2. 删除一棵二叉树 #

删除一棵二叉树相对简单，也是采用递归的算法，代码如下：

void dis(tree &bt){
    if(bt)
    dis(bt -> lchild);   //删除左子树
    dis(bt -> rchild);   //删除右子树
    delete bt;           //释放当前节点
}