主要内容 #

1. 机器数与真值
2. 原码表示
3. 反码表示
4. 补码表示
5. 总结

1. 机器数与真值 #

一个数在计算机中的表现形式叫做机器数，这个数有正负之分，在计算机中用一个数的最高位（符号位）用来表示它的正负，其中0表示正数，1表示负数。
例如：

正数7，在计算机中用一个8位的二进制数来表示:
00000111；
而负数-7，用一个8位的二进制数来表示:
10000111，
这里的00000111和10000111是机器数。

计算机中的机器数对应的真实的值就是真数，对最高位（符号位）后面的二进制数转换成10进制，并根据最高位来确定这个数的正负。
对于上面的00000111和10000111来说：

最高位（符号位）后面的二进制数转换成10进制：
0000111 ————> 7
最高位分别是 0 和 1，
结果就是    7 和 -7。

2. 原码表示 #

用第一位表示符号，其余位表示值。因为第一位是符号位，所以8位二进制数的取值范围就是：1111 1111 ~ 0111 1111 即-127 ~ 127。
原码是容易被人脑所理解的表达方式。
练习：将原码 0010 1010 和 1001 0101 转化为10进制表示的数。
答案：42 和 -21。

3. 反码表示 #

反码的表示方法是:

• 正数的反码是其本身；
• 负数的反码是在其原码的基础上, 符号位不变，其余各个位取反。

例如：

[+1] = [00000001]原 = [00000001]反
[-1] = [10000001]原 = [11111110]反

练习：写出10进制下的数字17和-11的原码和补码。
答案：[+17] = [0001 0001]原 = [0001 0001]反
[-11] = [1000 1011]原 = [1111 0100]反

4. 补码表示 #

补码的表示方法为：

• 正数的补码就是其本身；
• 负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1. (即在反码的基础上+1)

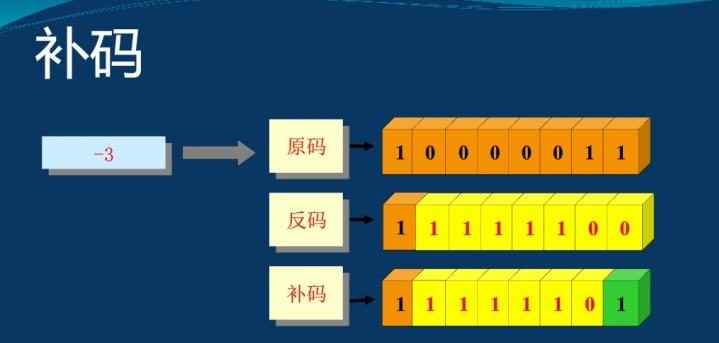
例如：

[+1] = [00000001]原 = [00000001]反 = [00000001]补
[-1] = [10000001]原 = [11111110]反 = [11111111]补

练习：写出10进制下的数字27和-51的原码、反码和补码。
答案：[+27] = [0001 1011]原 = [0001 1011]反 = [0001 1011]补
[-51] = [1011 0011]原 = [1100 1100]反 = [1100 1101]补

5. 总结 #

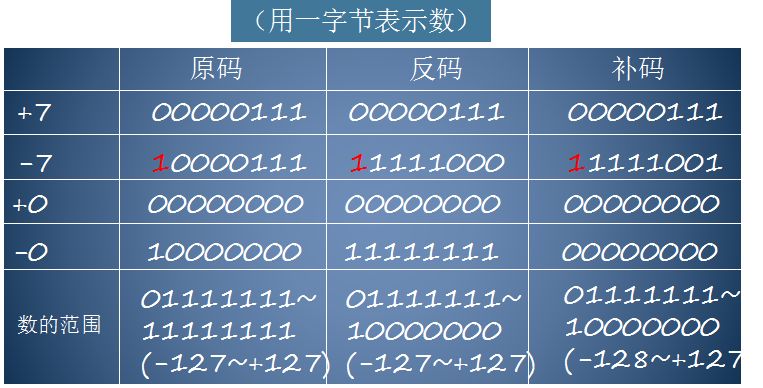
计算机可以有三种编码方式表示一个数。对于正数因为三种编码方式的结果都相同，但是对于负数三种编码方式的结果都不相同，真值0的反码和补码都不唯一，而补码表示是唯一的。

但是注意：[1000 0000]补 就是-128。-128并没有原码和反码表示。对-128的补码表示[1000 0000]补算出来的原码是[0000 0000]原, 这是不正确的。