跳至正文
View Categories

1 min read

主要内容 #

  1. 进位，错位处理
  2. 高精度乘法

1. 进位，错位处理 #

1.1高精度-单精度计算 #

先考虑一个简单的情况：乘数中的一个是普通的 int 类型。有没有简单的处理方法呢？
一个直观的思路是直接将a每一位上的数字乘以b。从数值上来说，这个方法是正确的，但它并不符合十进制表示法，因此需要将它重新整理成正常的样子。
重整的方式，也是从个位开始逐位向上处理进位。但是这里的进位可能非常大，甚至远大于9，因为每一位被乘上之后都可能达到9b的数量级。所以这里的进位不能再简单地进行-10运算，而是要通过除以10的商以及余数计算。详见代码注释，也可以参考下图展示的一个计算高精度数1337乘以单精度数42的过程。

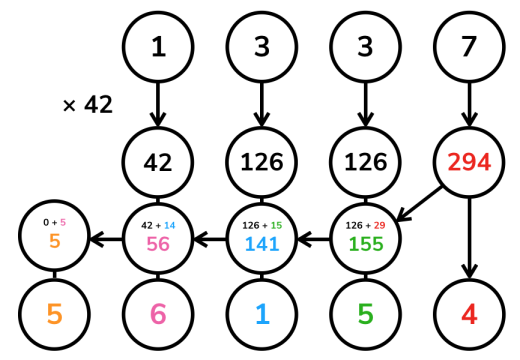
当然，也是出于这个原因，这个方法需要特别关注乘数b的范围。若它和 10^9（或相应整型的取值上界）属于同一数量级，那么需要慎用高精度—单精度乘法。

void mul_short(int a[], int b, int c[]) {
  clear(c);

  for (int i = 0; i < LEN - 1; ++i) {
    // 直接把 a 的第 i 位数码乘以乘数，加入结果
    c[i] += a[i] * b;

    if (c[i] >= 10) {
      // 处理进位
      // c[i] / 10 即除法的商数成为进位的增量值
      c[i + 1] += c[i] / 10;
      // 而 c[i] % 10 即除法的余数成为在当前位留下的值
      c[i] %= 10;
    }
  }
}

1.2高精度-高精度 #

如果两个乘数都是高精度，那么竖式乘法又可以大显身手。
于是可以将b分解为它的所有数码，其中每个数码都是单精度数，将它们分别与a相乘，再向左移动到各自的位置上相加即得答案。当然，最后也需要用与上例相同的方式处理进位。

注意这个过程与竖式乘法不尽相同，我们的算法在每一步乘的过程中并不进位，而是将所有的结果保留在对应的位置上，到最后再统一处理进位，但这不会影响结果。

void mul(int a[], int b[], int c[]) {
  clear(c);

  for (int i = 0; i < LEN - 1; ++i) {
    // 这里直接计算结果中的从低到高第 i 位，且一并处理了进位
    // 第 i 次循环为 c[i] 加上了所有满足 p + q = i 的 a[p] 与 b[q] 的乘积之和
    // 这样做的效果和直接进行上图的运算最后求和是一样的，只是更加简短的一种实现方式
    for (int j = 0; j <= i; ++j) c[i] += a[j] * b[i - j];

    if (c[i] >= 10) {
      c[i + 1] += c[i] / 10;
      c[i] %= 10;
    }
  }
}

2. 高精度乘法 #

请输入两个数，计算它们的积。

【算法分析】
竖式方法举例：

  • 25*836
int b[] = {2,5};
int a[] = {8,3,6};

            b1 b0
___x_____a2_a1_a0__
         c2 c1 c0
      d2 d1 d0     
___e2_e1_e0________
f5 f4 f3 f2 f1 f0


我们不妨改一下数据的下标，以便于更好的理解下面的代码。
            b1 b0
___x_____a2_a1_a0__
         c2 c1 c0
      d3 d2 d1     
___e4_e3_e2________
f5 f4 f3 f2 f1 f0

## 1 
fi 的计算过程推导，是代码实现的关键。
1. f的序号和ab有什么关系？为什么是【f序号 = a序号 + b序号】
2. fi的值，是一个累加过程。

## 2 
两数乘积的位数，如何确定？
f5 可能没有吗？

【例程】

#include < iostream >
#include < string >
using namespace std;


void multiply(int a[], int b[], int a_len, int b_len, int* f, int& f_len)
{
    int i = 0, x = 0;
    f_len = 0;

    for (int i = 0; i < a_len; ++i)
    {
        int x = 0; // x 表示进位
        for (int j = 0; j < b_len; ++j)
        {
            // 乘法核心代码
            f[i+j] += a[i] * b[j] + x;
            x = f[i+j] / 10;
            f[i+j] %= 10;
        }
        f[i + b_len] = x;
    }

    // 根据最后一位是否为 0 ，判断计算结果的位数
    if (f[a_len + b_len - 1] == 0)
        f_len = a_len + b_len - 1;
    else
        f_len = a_len + b_len;
}

int main()
{
    // 从屏幕获得输入
    string astr, bstr;
    cin >> astr;
    cin >> bstr;

    int lena = astr.size(), lenb = bstr.size();
    int a[100] = { 0 }, b[100] = { 0 }; // 假设数字的位数不超过 100
    for (int i = 0; i < lena; ++i)
        a[lena - i - 1] = astr[i] - '0'; // 将数字倒过来

    for (int i = 0; i < lenb; ++i)
        b[lenb - i - 1] = bstr[i] - '0';


    // 计算高精度乘法
    int f[100] = { 0 }, lenf(0);
    multiply(a, b, lena, lenb, f, lenf); // 必须是两个非负数，且 a 大于 b


    // 输出结果
    for (int i = 0; i < lenf; ++i)
    {
        cout << f[lenf - i - 1];
    }
    cout << endl;
    return 0;
}

习题 #

请将上面的例题，独立完成一遍。要求必须掌握。下节课要求每个人都能够独立写出上面的代码。
课后练习

What are your Feelings