主要内容 #

1. 枚举法的定义
2. 枚举法的计算步骤
3. 举例
4. 模拟法的概念
5. 模拟法解题思路
6. 举例

1.1 枚举法的定义 #

在进行归纳推理时，如果逐个考察了某类事件的所有可能情况，因而得出一般结论，那么该结论是可靠的，这种归纳方法叫做枚举法。由此可知，使用该算法需要满足两个条件：(1)可预先确定候选答案的数量；(2)候选答案的范围在求解之前必须有一个确定的集合。枚举在日常生活中很常见，例如“星期”这个词就是一个枚举，星期一、星期二、 星期三、星期四、星期五、星期六、星期日就是这个枚举里面的成员。
枚举算法的思想是：
将问题的所有可能的答案一一列举，然后根据条件判断此答案是否合适，保留合适的，舍弃不合适的。

2.1 枚举法的计算步骤 #

枚举算法简单粗暴，他暴力的枚举所有可能，尽可能地尝试所有的方法。虽然枚举算法非常暴力，而且速度可能很慢，但确实我们最应该优先考虑的！因为枚举法变成实现最简单，并且得到的结果总是正确的。其计算步骤为：
（1）确定解题的可能范围，不能遗漏任何一个真正解，同时避免重复。
（2）判定是否是真正解的方法。
（3）为了提高解决问题的效率，使可能解的范围将至最小。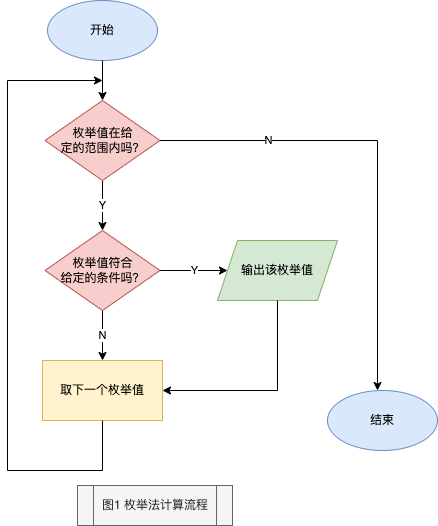

3.1 举例 #

问题描述：
公鸡每只5元，母鸡每只3元，三只小鸡1元，用100元买100只鸡，问公鸡、母鸡、小鸡各多少只？
算法分析：
利用枚举法解决该问题，以三种鸡的个数为枚举对象,分别设为mj,gj和xj，用三种鸡的总数 （mj+gj+xj=100）和买鸡钱的总数（1/3*xj+mj*3+gj*5=100）作为判定条件，穷举各种鸡的个数。
参考程序：

#include<iostream>
using namespace std;
int main()
{
	int mj=0, gj=0, xj=0;                  //定义变量分别表示母鸡、公鸡、小鸡并初始化
	for (gj = 0; gj <= 20; gj++)		   //公鸡最多可买20个
	{
		for (mj = 0; mj <= 33; mj++)	   //母鸡最多可买33个
		{
			xj = 100 - gj - mj;			   // 三种鸡的总数是100只
			if (xj % 3 == 0 && 5 * gj + 3 * mj + xj / 3 == 100)// 总花费为100元
		    printf("公鸡为 %d 只，母鸡为 %d 只，小鸡为 %d 只！\n", gj, mj, xj);
		}
	}
	return 0;
}

统计方形 #

问题描述
有一个 nxm 方格的棋盘，求其方格包含多少正方形、长方形（不包含正方形）。
1.2 输入格式
一行，两个正整数 n,m（n≤5000,m≤5000）。
1.3 输出格式
一行，两个正整数，分别表示方格包含多少正方形、长方形（不包含正方形）。
1.4 输入输出样例
输入
2 3
输出
8 10
1.5 分析
矩形包含长方形和正方形，因此可以算出棋盘有多少个矩形，再找出有多少个正方形，两个相减就可以算出长方形的个数。这里枚举的方法比较多，可以枚举点，也可以枚举边。
这里以枚举边为例。横向所有可能的边长为((n + 1) * n) / 2，纵向所有可能的边长为((m + 1) * m) / 2，则棋盘包含的所有的矩形个数为两式相乘。再计算正方形的个数，正方形最大边长一定是m和n中的较小的那一个，于是再循环枚举所有可能的正方形边长，即1、2、3、…、min(m，n)，再相减就能得到长方形的个数。
1.6 参考代码

#include<iostream>
#include<algorithm>
using namespace std;
int main()
{
    long long n, m;
    long long seq = 0;  //正方形个数
    long long rec, sum;  //长方形个数、矩形总个数
    cin >> n;
    cin >> m;
    long long x = n;
    long long y = m;
    sum = (((n + 1) * n) / 2) * (((m + 1) * m) / 2);
    for(int i = 1; i <= min(m, n); i++)
    {
        seq += x * y;
        x--;
        y--;
    }
    rec = sum - seq;
    cout << seq << ' ' << rec << endl;
    return 0;
}

  #

涂国旗 #

问题描述
某国法律规定，只要一个由 N×M 个小方块组成的旗帜符合如下规则，就是合法的国旗。

1. 从最上方若干行（至少一行）的格子全部是白色的；
2. 接下来若干行（至少一行）的格子全部是蓝色的；
3. 剩下的行（至少一行）全部是红色的；

现有一个棋盘状的布，分成了 N行 M列的格子，每个格子是白色蓝色红色之一，小 a 希望把这个布改成该国国旗，方法是在一些格子上涂颜料，盖住之前的颜色。
小a很懒，希望涂最少的格子，使这块布成为一个合法的国旗。
2.2 输入格式
第一行是两个整数 N,M（N,M≤50）。
接下来 N 行是一个矩阵，矩阵的每一个小方块是W（白），B（蓝），R（红）中的一个。
2.3 输出格式
一个整数，表示至少需要涂多少块。
2.4 输入输出样例
输入
4 5
WRWRW
BWRWB
WRWRW
RWBWR
输出
11
2.5 分析
首先，三种颜色都要占一行，然后从边界开始枚举每一种情况所需要操作的次数，记录最小值
2.6 参考代码

#include<iostream>
#include<algorithm>
#define N 55
using namespace std;
char flag[N][N];
int min_num = 10000;  //存储最小的涂装数目，初始值一定是一个足够大的数
int main()
{
    int n, m;
    int step;
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= m; j++)
            cin >> flag[i][j];      //输入旗子原本的颜色
    }
    for(int i = 1; i <= n - 2; i++)  //白与蓝的边界
    {
        for(int j = i + 1; j <= n - 1; j++)  //蓝与红的边界
        {
            step = 0;
            //开始枚举
            for(int k = 1; k <= i; k++)
                for(int l = 1; l <= m; l++)
                {
                    if(flag[k][l] != 'W')
                        step++;
                }
            for(int k = i + 1; k <= j; k++)
                for(int l = 1; l <= m; l++)
                {
                    if(flag[k][l] != 'B')
                        step++;
                }
            for(int k = j + 1; k <= n; k++)
                for(int l = 1; l <= m; l++)
                {
                    if(flag[k][l] != 'R')
                        step++;
                }
            min_num = min(min_num, step);
        }
    }
    cout << min_num;
    return 0;
}

  #

2.1 模拟法的概念 #

自然界和日常生活中的有些事物，很难建立数学模型，我们解决这类问题可用模拟法。所谓模拟法，就是用计算机模拟某个过程，通过改变数学模型的各种参数，进而观察变更这些参数所引起的过程状态的变化，然后从中得出解答。
由于模拟法往往是从实际工程应用中提取出来的一些核心问题，或者本身就是某个工程的简化模型，所以解答模拟题特别需要有良好的理解能力、分析能力和规划能力。模拟题的算法一般都不太复杂，关键是所有条件都不能遗漏并要把条件分析清楚。求解模拟题一般都比较繁琐，编程前一定要预先规划好各个模块的功能和结构，以免具体编程时注意了局部而遗漏了某些重要的方面。

2.2 模拟法的求解思路 #

解答模拟题通常的步骤是：
（1）认真仔细的读懂题目。模拟题的描述通常都比较详细，篇幅一般都比较长，应该边阅读边将有关的条件一条条地记录下来，阅读完成后要反复核对，绝对不能有错漏。
（2）建立各个条件之间的关系，最好用一些简明的表格列出。
（3）认真分析这些关系，并建立这些关系的数学模型。
（4）规划各个模块的结构，用相应的语言、逐步求精的方法描述具体的算法。
（5）编写程序，调试并运行。
（6）检查题目给出的样例能否通过。竞赛题目中一般都会给出输入输出样例，以便检查程序的输入输出格式是否正确，但这些样例往往会比竞赛时评判所用的测试数据简单，所以你不能满足于通过这些样例，还要尽量自拟一些更复杂、更全面的测试数据来检查程序的正确性。经过反复的调试、检查，才算完成该题。

2.3 举例 #

陶陶家的院子里有一棵苹果树，每到秋天树上就会结出 10个苹果。苹果成熟的时候，陶陶就会跑去摘苹果。陶陶有个 30厘米高的板凳，当她不能直接用手摘到苹果的时候，就会踩到板凳上再试试。
现在已知 10个苹果到地面的高度，以及陶陶把手伸直的时候能够达到的最大高度，请帮陶陶算一下她能够摘到的苹果的数目。假设她碰到苹果，苹果就会掉下来。
输入格式
输入包括两行数据。第一行包含 10 个 100 到 200 之间（包括 100 和 200 ）的整数（以厘米为单位）分别表示 10 个苹果到地面的高度，两个相邻的整数之间用一个空格隔开。第二行只包括一个 100 到 120 之间（包含 100和 120 ）的整数（以厘米为单位），表示陶陶把手伸直的时候能够达到的最大高度。
输出格式
输出包括一行，这一行只包含一个整数，表示陶陶能够摘到的苹果的数目。
输入输出样例
输入

100 200 150 140 129 134 167 198 200 111
110

输出

5

参考代码

#include <iostream>
using namespace std;
int a[20],h,s;
int main(){
    for(int i=0;i<10;i++)cin >> a[i]; //输入数据
    cin>>h; //输入高度
    h+=30;  //站上板凳上的高度
    for(int i=0;i<10;i++)s+=!(h<a[i]); //如果高度够了结果就加一
    cout<<s;//输出结果
    return 0;
}

  #

铺地毯 #

1.1 问题描述
为了准备一个独特的颁奖典礼，组织者在会场的一片矩形区域（可看做是平面直角坐标系的第一象限）铺上一些矩形地毯。一共有 n 张地毯，编号从 1 到 n。现在将这些地毯按照编号从小到大的顺序平行于坐标轴先后铺设，后铺的地毯覆盖在前面已经铺好的地毯之上。地毯铺设完成后，组织者想知道覆盖地面某个点的最上面的那张地毯的编号。注意：在矩形地毯边界和四个顶点上的点也算被地毯覆盖。
1.2 输入格式
输入共 n+2 行。第一行，一个整数 n，表示总共有 n 张地毯。接下来的 n 行中，第 i+1 行表示编号 i 的地毯的信息，包含四个正整数 a，b，g，k，每两个整数之间用一个空格隔开，分别表示铺设地毯的左下角的坐标（a，b）以及地毯在 x轴和 y 轴方向的长度。第 n+2 行包含两个正整数 x 和 y，表示所求的地面的点的坐标（x，y）。
1.3 输出格式
输出共1行，一个整数，表示所求的地毯的编号；若此处没有被地毯覆盖则输出-1
1.4 输入输出样例
输入
3
1 0 2 3
0 2 3 3
2 1 3 3
2 2
输出
3
1.5 分析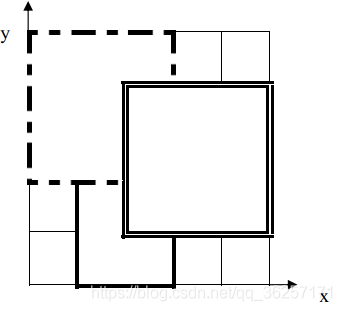

如上图，1 号地毯用实线表示，2 号地毯用虚线表示，3 号用双实线表示，覆盖点(2,2)的最上面一张地毯是 3 号地毯。那么我们可以使用 for循环 和 if判断语句 来解答此题。
1.6 参考代码

#include<iostream>                         //比赛可用C++万能头文件，也可用iostream库
using namespace std;                        
int a[10002],b[10002],g[10002],k[10002];       //定义数组;
int main()                                    
{
    int n,x,y,i,s=-1;                       //注意：由题可得，这里的累加器最初应定义-1
    cin>>n;
    for(i=1;i<=n;i++)
    {
    cin>>a[i]>>b[i]>>g[i]>>k[i];         //通过for循环输入
    }
    cin>>x>>y;
    for(i=1;i<=n;i++)
    {
    if(x>=a[i]&&x<=a[i]+g[i]&&
       y>=b[i]&&y<=b[i]+k[i])        //判断语句
       s=i;
    }
    cout<<s;
    return 0;                     //结束整个程序
}

  #

津津的储蓄计划 #

2.1 问题描述
津津的零花钱一直都是自己管理。每个月的月初妈妈给津津300元钱，津津会预算这个月的花销，并且总能做到实际花销和预算的相同。
为了让津津学习如何储蓄，妈妈提出，津津可以随时把整百的钱存在她那里，到了年末她会加上20%还给津津。因此津津制定了一个储蓄计划：每个月的月初，在得到妈妈给的零花钱后，如果她预计到这个月的月末手中还会有多于100元或恰好100元，她就会把整百的钱存在妈妈那里，剩余的钱留在自己手中。
例如11月初津津手中还有83元，妈妈给了津津300元。津津预计11月的花销是180元，那么她就会在妈妈那里存200元，自己留下183元。到了11月月末，津津手中会剩下3元钱。
津津发现这个储蓄计划的主要风险是，存在妈妈那里的钱在年末之前不能取出。有可能在某个月的月初，津津手中的钱加上这个月妈妈给的钱，不够这个月的原定预算。如果出现这种情况，津津将不得不在这个月省吃俭用，压缩预算。
现在请你根据2004年1月到12月每个月津津的预算，判断会不会出现这种情况。如果不会，计算到2004年年末，妈妈将津津平常存的钱加上20％还给津津之后，津津手中会有多少钱。
2.2 输入格式
12行数据，每行包含一个小于350的非负整数，分别表示1月到12月津津的预算。
2.3 输出格式
一个整数。如果储蓄计划实施过程中出现某个月钱不够用的情况，输出−X，X表示出现这种情况的第一个月；否则输出到2004年年末津津手中会有多少钱。
2.4 输入输出样例
输入
290
230
280
200
300
170
340
50
90
80
200
60
输出
-7
2.5 参考程序

#include<iostream>
using namespace std;
int a = 0, sum = 0; //表示目前津津手上的钱，sum 表示存在妈妈那里的錢
int main(){   
    int month;   //month 表示每月的开支
    for(int i = 1; i <= 12; ++i){
        cin >> month;
        a += 300;       //每月得到的零花钱
        if(a < month){    //判断手上的钱对于开支是否足够
            cout << -i << endl;  //如果不足则输出“-”加月份
            return 0;     //如果不足，输出后结束程序
        }
        a -= month;    //如果够减去开支
        if(a >= 100){
            sum += 100*(a/100);//再把剩下的钱足整百的部分存入（加上a减去其除100的余数 即整百数）
            a %= 100; //计算剩下的钱（因整百部分被存入，故a=其除以100后的余数）
        }
    }
    cout << sum*1.2 + a << endl; //说明没有钱不足的情况，故应输出120%的储蓄加上手头的钱
    return 0;
}

练习 #

枚举元组

特别数的和

最长连号

开灯