引例 #
1. 递推算法概述 #
一个问题的求解需一系列的计算,在已知条件和所求问题之间总存在着某种相互联系的关系,在计算时如果可以找到前后过程之间的数量关系(即递推式),那么,从问题出发逐步推到已知条件,此种方法叫逆推。无论顺推还是逆推,其关键是要找到递推式。这种处理问题的方法能使复杂运算化为若干步重复的简单运算,充分发挥出计算机擅长于重复处理的特点。
递推算法的首要问题是得到相邻的数据项间的关系(即递推关系)。递推算法避开了求通项公式的麻烦,把一个复杂问题的求解,分解成了连续的若干步简单运算。一般说来,可以将递推算法看成是一种特殊的迭代算法。
2. 数塔问题 #
如下所示为一个数字三角形。请编一个程序计算从顶到底的某处的一条路径,使该路径所经过的数字总和最大。只要求输出总和。
1、 一步可沿左斜线向下或右斜线向下走;
2、 三角形行数小于等于100;
3、 三角形中的数字为0,1,…,99;
测试数据通键盘逐行输入,如上例数据应以如下所示格式输入:
5
7 7
3 8 3 8
8 1 0 8 1 0
2 7 4 4 2 7 4 4
4 5 2 6 5 4 5 2 6 5
输入的数据
3. 算法分析 #
从递推的思想出发,设想,当从顶层沿某条路径走到第i层向第i+1层前进时,我们的选择一定是沿其下两条可行路径中最大数字的方向前进,为此,我们可以采用倒推的手法,设a[i][j]存放从i,j 出发到达n层的最大值,则a[i][j]=max{a[i][j]+a[i+1][j],a[i][j]+a[i+1][j+1]},a[1][1] 即为所求的数字总和的最大值。
4. 参考程序 #
#include < iostream >
using namespace std;
int main(){
int n, i, j, a[101][101];
//输入数塔的行数n
cin >> n;
//逐行输入数据
for(i = 1; i <= n; ++i){
for(j = 1; j <= i; ++j){
cin >> a[i][j];
}
}
//采用倒推的手法,从底层往上推
for(i = n - 1; i >= 1; i--){
for(j = 1; j <= i; j++){
if(a[i + 1][j] >= a[i + 1][j + 1]){
a[i][j] += a[i + 1][j];
}else{
a[i][j] += a[i + 1][j + 1];
}
}
}
//输出结果
cout << a[1][1] << endl;
return 0;
}
例题 #
- 斐波那契数列
- 走台阶
- 不回头走法
- 拉灯
斐波那契数列 #
1. 问题的提出 #
在西方,最先研究这个数列的人是比萨的列奥那多(意大利人斐波那契Leonardo Fibonacci),他描述兔子生长的数目时用上了这数列:
- 第一个月初有一对刚诞生的兔子
- 第二个月之后(第三个月初)它们可以生育
- 每月每对可生育的兔子会诞生下一对新兔子
- 兔子永不死去
假设在n月有兔子总共a对,n+1月总共有b对。在n+2月必定总共有a+b对:因为在n+2月的时候,前一月(n+1月)的b对兔子可以存留至第n+2月(在当月属于新诞生的兔子尚不能生育)。而新生育出的兔子对数等于所有在n月就已存在的a对
Fibonacci 数列的表达式为:
F(1)=1
F(2)=1
F(n) = F(n-1)+F(n-2)(n≥3)
经过计算,Fibonacci 数列的通项公式为: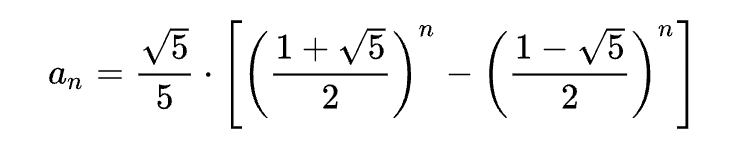
2. 深层的含义 #
2.1 黄金分割数列 #
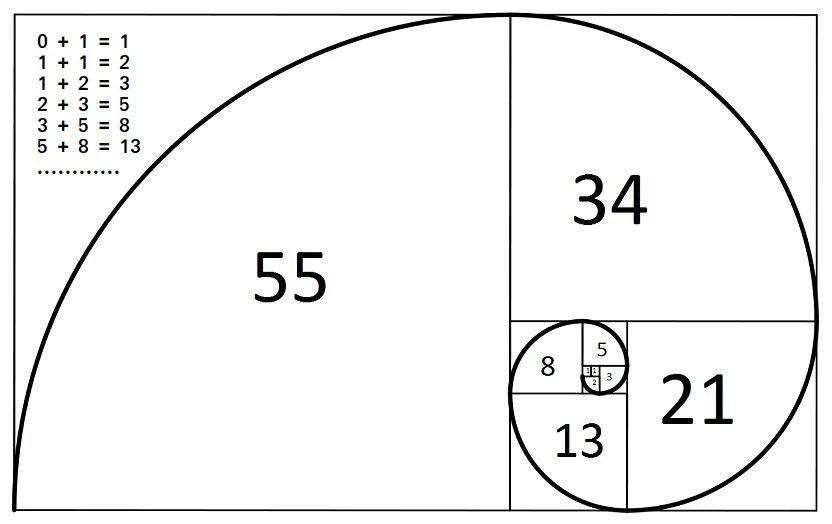
Fibonacci数列也被称为黄金分割数列,以Fibonacci数列为边长的正方形拼成的长方形越来越接近于黄金矩形(1:1.618)。
1、 1、 2、 3、 5、 8、 13、 21、 34、 55、 89、 144、 233、 377、 610、 987……
2.2 杨辉三角形 #
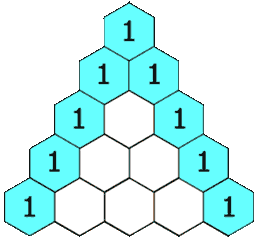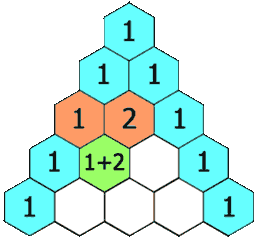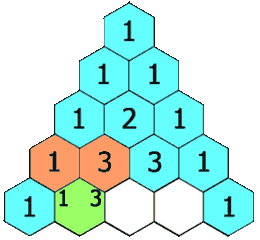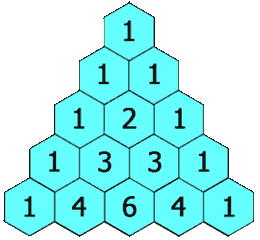

每个数是它左上方和右上方的数的和。
斐波纳契数也是杨辉三角形的每一条红色对角线上数字的和。
2.3 植物的生长 #
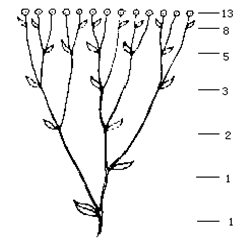
有些植物在生长点,即树枝形成或分裂的地方表达斐波那契数列。一个枝干生长后产生分支,会产生两个生长点。接下来,主枝干生成另一个分支,从而产生三个增长点。然后树干和第一分支产生两个增长点,使总数达到五个。此模式继续遵循斐波那契数。
植物按照这样的方式生长将有利于进行光合作用。
此外,如果你计算花上的花瓣数,通常会发现花瓣的总数就是斐波那契数列中的数字之一。例如,百合和鸢尾有三个花瓣,金凤花和野玫瑰有五个花瓣,飞燕草有八瓣等等。
还有菠萝、松子等,也都符合这个特点,一般会出现34,55,89和144这几个数字。
Fibonacci数列虽然简单但是是数学当中非常重要的数列。
3. 算法求解 #
#include < iostream >
using namespace std;
int main(){
int x, y, n;
x = 1;
y = 0;
for(int i = 0; i < n; ++i){
x = x + y;
y = x - y;
}
cout << y << endl;
return 0;
}
走台阶 #
请思考以下问题,并动手编写程序:
楼梯有n个台阶,上楼可以一步上一个台阶,也可以一步上两个台阶。一共有多少种上楼的方法?
1. 问题分析 #
- 假设有1个台阶,只有1种方法:
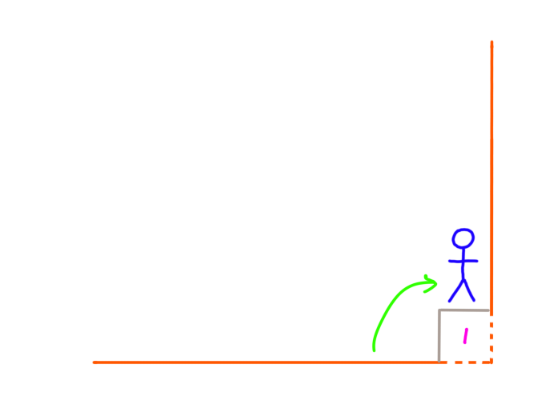
- 假设有2级台阶,只有2种方法:
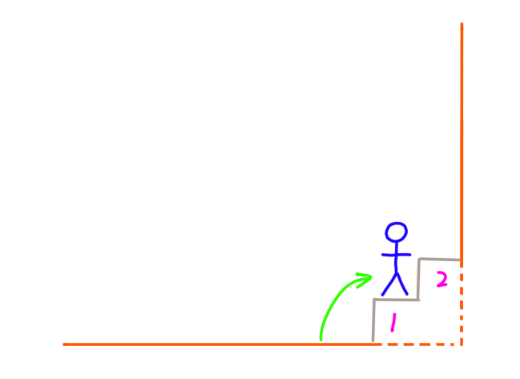
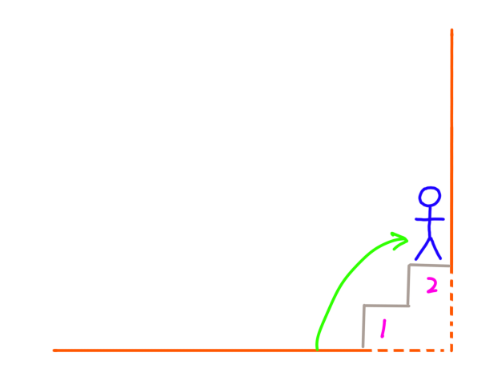
- 假设有3级台阶
3.1 先爬1阶,接下来还有2阶台阶,那问题就是有2阶台阶怎么爬:
3.2 先爬2阶,接下来还有1阶台阶,那问题就是有1阶台阶怎么爬: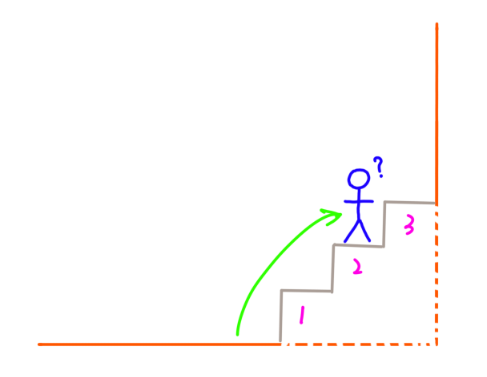
- 假设有n级台阶
4.1 先爬1阶,接下来还有 n – 1 阶台阶,那问题就是有n – 1阶台阶怎么爬: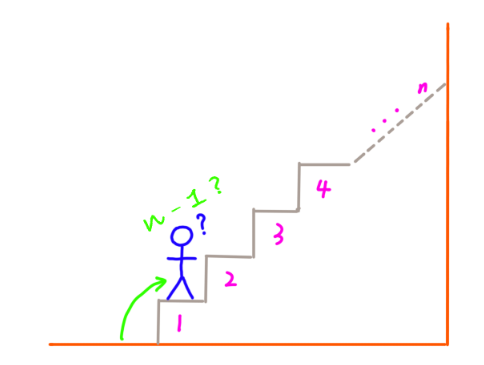
4.2 先爬2阶,接下来还有 n – 2 阶台阶,那问题就是有n – 2阶台阶怎么爬: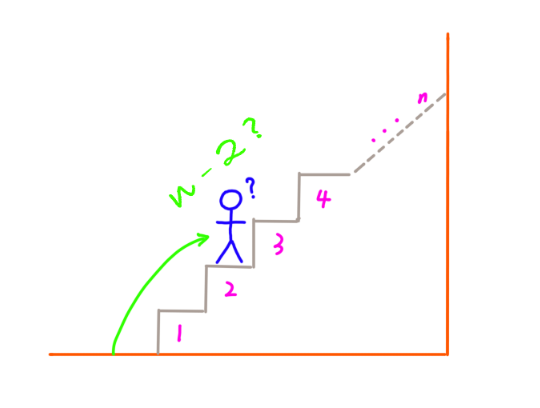
数学归纳法得出,有n阶台阶那么就是 n – 1 阶台阶和 n – 2 阶台阶爬上楼顶的方法的和。
公式: f(n) = f(n – 1) + f(n – 2) , 这不就是菲波那切数列数量求和吗?
2. 编程求解 #
#include < iostream >
#include < vector >
using namespace std;
int climbStairs(int n) {
//建立容器
vector dp(n+1, 0);
//设定边界值
dp[0]=1;
dp[1]=1;
//循环求解
for(int i=2;i<=n;i++){
dp[i]=dp[i-1]+dp[i-2];
}
return dp[n];
}
int main(){
int n;
cin >> n;
cout << climbStairs(n) << endl;
return 0;
}

算法优化
使用容器占用较大的空间,可以用p,q,r三个变量循环代替容器。
#include < iostream >
using namespace std;
int climbStairs(int n) {
int p = 0, q = 0, r = 1;
for (int i = 1; i <= n; ++i) {
p = q;
q = r;
r = p + q;
}
return r;
}
int main(){
int n;
cin >> n;
cout << climbStairs(n) << endl;
return 0;
}
不回头走法 #
1. 问题介绍 #
从原点出发,一步只能向右走、向上走或向左走。恰好走N步且不经过已走的点共有多少种走法?
样例输入:N=2
样例输出:result=7
样例输入:N=3
样例输出:result=17
2. 求解方法 #
解题思路:要解决走N步共有多少种走法,我们在拿到题目的时候最直接的想法就是先画出当N=1、N=2、N=3。。。。。N=n时对应走法的图例,由简单到复杂、由特殊到一般的推理过程,找出规律获得解题的思路。在数学上,我们称为归纳法。如果用编程的方法来求解这样的推理题,我们把这样的求解思路(算法)称之为递推法。递推的精髓在于f(n)的结果一般由f(n-1)、f(n-2)…..f(n-k)的前k次结果推导出来。我们在解决这类递推问题时,难点就是如何从简单而特殊的案例,找到问题的一般规律,写出f(n)与f(n-1)、f(n-2)…..f(n-k)之间的关系表达式,从而得出求解的结果。
(1) 当N=1时,绘出走法图
共有3种不同的走法,也就是黑色线条的数量,即f(1)=3
(2) 当N=2时,绘出走法图
共有7种不同的走法,也就是绿色线条的数量,即f(2)=7
(3) 当N=3时,绘出走法图
共有17种不同的走法,也就是红色线条的数量,即f(3)=17
由此,我们不难看出,对于任何一个起点,最多可以走出3种走法,但最少必须走出2种走法。那么我们要求出f(n),实际上转换为如果我们能够得到上一步即f(n-1)有多少个终点是有3种走法的,有多少个点有2种走法的,那么问题就解决了。
a. 上一步,即f(n-1)有多少个终点是有3种走法的。
对于N=3时,f(n-1)=f(2), 有3个点A、B、C可以走出3种不同走法的,这3个点是怎么得到的呢?它的存在与N值有没有必然的联系?如果我们能找到它与N之间的关系,问题也就解决了。有了这样的思路以后,我们不难找到这样的规律:如果f(n-2)存在,即上上步存在,那么从上上步出发的线路里面必然会有一条向上走的线路,而这条向上走的线路在到达f(n-1)之后, 向f(n)出发时也必然有左、上、右这三种走法,那么我们就得出了这样的结论:当f(n-2)存在时,f(n-2)的值实际上就等价于f(n-1)有多少个终点是有3种走法。
b. f(n-1)有多少个终点是有2种走法的
对于N=3时,有4个点D、E、F、G可以走出2种不同走法的,这4个点又是怎么得到的呢?它与N值有什么联系呢? 实际上我们在解决了上一个问题的时候,这个问题就变得相当容易了, f(n-1)减掉刚才有3种走法的点,剩下的点不就是只有2种走法了吗?即f(n-1)-f(n-2)。
c. 得出f(n)的一般关系式
f(n)=3f(n-2)+2(f(n-1)-f(n-2) ) (n>=3)
化简:
f(n)=2*f(n-1)+f(n-2) (n>=3)
3. 编程计算 #
#include <stdio.h>
#include <windows.h>
int main()
{
int n;
int i;
int fn_1,fn_2;
printf("please input n=");
scanf("%d",&n); //输入任意n值
int fn=0;
if(n==1)
fn=3; //初始化当n=1和n=2时的临界条件
else if(n==2)
fn=7;
else{
fn_1=7;
fn_2=3;
for(i=3;i<=n;i++)
{
fn=2*fn_1+fn_2; //当n>=3时fn的通式
fn_2=fn_1;//更新fn_1和fn_2的值
fn_1=fn;
}
}
printf("一共有%d种走法!\n",fn); //输出结果
return 0;
}
拉灯 #
1. 问题介绍 #
你玩过“拉灯”游戏吗?25盏灯排成一个 5×5 的方形。每一个灯都有一个开关,游戏者可以改变它的状态。每一步,游戏者可以改变某一个灯的状态。游戏者改变一个灯的状态会产生连锁反应:和这个灯上下左右相邻的灯也要相应地改变其状态。我们用数字1表示一盏开着的灯,用数字0表示关着的灯。
下面这种状态:
10111 01101 10111 10000 11011
在改变了最左上角的灯的状态后将变成:
01111 11101 10111 10000 11011
再改变它正中间的灯后状态将变成:
01111 11001 11001 10100 11011
给定一些游戏的初始状态,编写程序判断游戏者是否可能在6步以内使所有的灯都变亮。
输入格式
第一行输入正整数n,代表数据中共有n个待解决的游戏初始状态。
以下若干行数据分为n组,每组数据有5行,每行5个字符。
每组数据描述了一个游戏的初始状态。
各组数据间用一个空行分隔。
输出格式
一共输出n行数据,每行有一个小于等于6的整数,它表示对于输入数据中对应的游戏状态最少需要几步才能使所有灯变亮。
对于某一个游戏初始状态,若6步以内无法使所有灯变亮,则输出−1。
输入样例
3 00111 01011 10001 11010 11100 11101 11101 11110 11111 11111 01111 11111 11111 11111 11111
输出样例
3 2 -1
2. 求解方法 #
首先有几点点很重要的性质需要说明:
- 如果按哪些灯确定了,那么按这些灯的顺序不重要,无论什么顺序,结果都是相同的
- 我们没有必要按一盏灯两次及以上,因为,按两次,相当于没按,按三次,相当于按两次+一次(也就是一次)
因此:
因为按灯的顺序不重要,我们可以先把第一行的灯都按了我们发现,第一行想按的灯都按过之后,如果想要让第一行全亮,那么我第二行只能有一种按法,就是按第一行不亮的灯的下面的灯(下面是例子)
第一行状态 10011 (1代表亮的灯) 第二行动作 01100 (1代表按按钮)
那么,我们怎么保证第二行全亮呢?只能用第三行来解决!
那么,我们怎么保证最后一行(第五行)全亮呢?没法保证!
发现,如果第一行按法确定了,那么接下来二三四五行的按法和能不能全亮就确定了。
因此,对于任意一种输入状态,我们把第一行 32 种按法全部遍历一遍,看看哪些可以全亮(通过检测第五行状态),这些全亮的种有没有操作次数小于等于6的。有的话,就返回这个操作数,否则就返回-1。
3. 编程计算 #
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 5 + 5; // 加上 5 更保险
// 注意接收时用字符串更方便,因为输入流每行没有空格
char g[N][N]; // 记录灯目前的情况
// 上右下左中
int dx[5] = {0, 1, 0, -1, 0};
int dy[5] = {1, 0, -1, 0, 0};
// 按第 x 行第 y 列,本身和上下左右五个灯都取反
void turn(int x, int y)
{
for (int i = 0; i < 5; ++ i)
{
int a = x + dx[i], b = y + dy[i];
if (0 <= a && a < 5 && 0 <= b && b < 5)
g[a][b] = g[a][b] == '1' ? '0': '1';
}
}
int work()
{
int ans = 2e9;
// 第一层循环,把所有第一行按的情况都遍历
// k 是被压缩了的状态,最小 0b00000 代表都不按,
// 最大 0b11111 代表都按
// 备份,因为下面的操作会改变 g
char backup[N][N];
memcpy(backup, g, sizeof g);
for (int k = 0; k < (1 << 5); ++ k)
{
// 确保我们的 g 是输入的 g
memcpy(g, backup, sizeof backup);
// 当第一行为 k 时,总操作次数是..
int res = 0; // 用 res 来记录
// 执行 k (根据 k 把第一行按了)
for (int j = 0; j < 5; ++ j)
{
if (k << j & 1)
{
res ++;
turn(0, j);
}
}
// 第一行确定了,第二行就确定了
// 因为只有合理操作第二行
// 才能把第一行全部点亮
// 以此类推,第二行定了后,第三行就被第二行决定了
for (int i = 0; i < 4; ++ i)
{
for (int j = 0; j < 5; ++ j)
{
if (g[i][j] == '0')
{
res ++;
turn(i + 1, j);
}
}
}
// 上面的操作一定能保证前 4 行全亮
// 但是第 5 行不一定全亮,第 5 行全亮,才是真正有效的操作
bool success = true;
for (int j = 0; j < 5; ++ j)
{
if (g[4][j] == '0')
{
success = false;
break;
}
}
// 如果是有效的操作,咱看看一共按了几次开关
if (success) ans = min(res, ans);
}
// 根据题意返回输出值
if (ans < 6) return -1;
return ans;
}
int main()
{
int n;
cin >> n;
while (n -- )
{
for (int i = 0; i < 5; ++ i) cin >> g[i];
printf("%d\n", work());
}
}



