跳至正文
View Categories

4 min read

引例 #

1. 递归算法概述 #

递归指的是在函数的定义中使用函数自身的方法。
举个例子：
从前有座山，山里有座庙，庙里有个老和尚，正在给小和尚讲故事呢！故事是什么呢？”从前有座山，山里有座庙，庙里有个老和尚，正在给小和尚讲故事呢！故事是什么呢？’从前有座山，山里有座庙，庙里有个老和尚，正在给小和尚讲故事呢！故事是什么呢？……'”
语法结构

void recursion()
{
   statements;
   ... ... ...
   recursion(); /* 函数调用自身 */
   ... ... ...
}
 
int main()
{
   recursion();
}

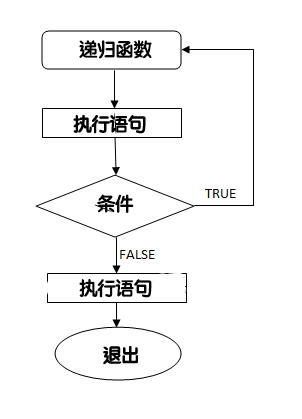
如下图所示：

程序员需要注意定义一个从函数退出的条件，否则会进入死循环。递归函数在解决许多数学问题上起了至关重要的作用，比如计算一个数的阶乘、生成斐波那契数列，等等。

2. 阶乘问题 #

算法分析
后一项之积=前一项之积*当前项，而前一项的计算方式与其相同，只是数据不同。s(n) = s(n-1)*n。
结束条件是n=1,此时s(1)=1。
下面的实例使用递归函数计算一个给定的数的阶乘：

#include < stdio.h >
 
double factorial(unsigned int i)
{ 
   //满足条件直接返回
   if(i <= 1)
   {
      return 1;
   }
   return i * factorial(i - 1);
}
int  main()
{
    int i = 15;
    printf("%d 的阶乘为 %f\n", i, factorial(i));
    return 0;

当上面的代码被编译和执行时，它会产生下列结果：

15 的阶乘为 1307674368000.000000

3. 算法优缺点 #

代码更简洁清晰，可读性好。
由于递归需要系统堆栈，所以空间消耗要比非递归代码要大很多。而且，如果递归深度太大，可能系统撑不住。
尽管有许多数学函数均可以递归表示，但在实际应用中，递归定义的高开销往往会让人望而却步。

例题 #

斐波那契数列算法 #

斐波那契数列以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：
1、1、2、3、5、8、13、21、34、……
在数学上，斐波纳契数列以如下被以递推的方法定义：
F(1)=1，F(2)=1,，F(n) = F(n-1) + F(n-2)（n>=3）。
问题分析： 斐波那契数列的对于原问题F(n)的求解可以转为对F(n-1)、F(n-2)两个子问题的求解，故符合条件（1）。由F(1)=1，F(2)=1,可以得出斐波那契数列问题是有递归出口的，递归出口对应F(1) = 1，F(2) = 1。

编程求解 #

求解斐波那契数列的C语言代码如下：

#include < stdio.h >
int fibonaci(int i)
{
   if(i == 0)
   {
      return 0;
   }
   if(i == 1)
   {
      return 1;
   }
   return fibonaci(i-1) + fibonaci(i-2);
}
 
int  main()
{
    int i;
    for (i = 0; i < 10; i++)
    {
       printf("%d\t\n", fibonaci(i));
    }
    return 0;
}

当上面的代码被编译和执行时，它会产生下列结果：

0    
1    
1    
2    
3    
5    
8    
13    
21    
34

请同学上面的C风格的代码，改写为C++风格的代码。
算法缺点：
由于使用递归时，其执行步骤是：要得到后一个数之前必须先计算出之前的两个数，即在每个递归调用时都会触发另外两个递归调用，例如：要得到F(10)之前得先得到F(9)、F(8)，那么得到F(9)之前得先得到F(8)、F(7)……如此递归下去。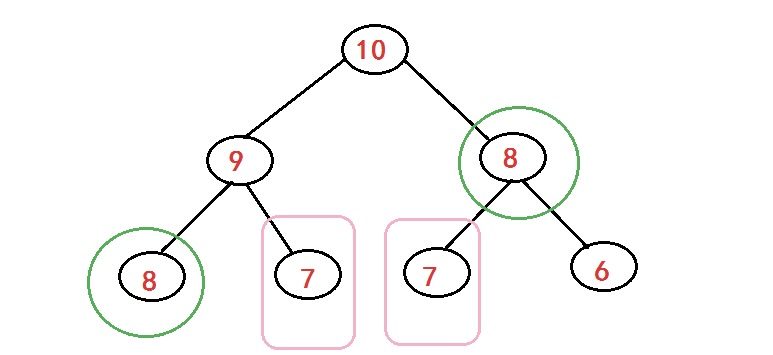

从上图可以看出，这样的计算是以 2 的次方在增长的。除此之外，也可以看到，F(8)和F(7)的值都被多次计算，如果递归的深度越深，那么F(8)和F(7)的值会被计算更多次，但是这样计算的结果都是一样的，除了其中之一外，其余的都是浪费，可想而知，这样的开销是非常恐怖的！

集合划分 #

设S是一个具有n个元素的集合，S = {a1, a2, ···, an}，现将S划分成k个满子集合S1, S2, ···, Sk，并且满足：

  1. 任意一个集合不为空；
  2. 任意一个元素不可能同时存在两个子集合中；
  3. 所有的元素均必须被分配。
    则称S1, S2, ···, Sk是集合S的一个划分，它相当于把S集合中的n个元素a1, a2, ···, an放入k个无标号的盒子中，使得没有一个盒子为空请你确定n个元素a1, a2, ···, an，放入k个无标号的盒子中的划分数S(n,k)。
    实际上这个问题的求解方法与之前的122课中第二类Stirling数求解方法完全一样。

算法分析 #

先举个例子，设S={1, 2, 3, 4}, k = 3,不难看出S有6种不同的划分方案，即S(4, 3) = 6。具体方案如下：
{1,2}{3}{4}
{1,3}{2}{4}
{1,4}{2}{3}
{2,3}{1}{4}
{2,4}{1}{3}
{3,4}{1}{2}
考虑一般情况，对于任意的含n个元素的a1, a2, ···, an的集合S，放入k个无标号的盒子中去，划分数为S(n,k)，凭直觉和经验很难划分和枚举划分的所有方案，必须归纳出问题的本质。其实对于任意一个元素an，必然有以下两种情况：

  1. {an}是其中一个子集，于是我们只需要把a1, a2, ···, an-1个元素划分到k-1个子集中，便解决了本题，这种强况下划分数共有S(n-1, k-1)个；
  2. {an}不是k个子集中的一个，则an必须和其他元素构成一个子集。则问题相当于先把a1, a2, ···, an-1划分成k个子集，这种情况下划分数共有S(n-1, k)个；然后再把an加入到k个子集中的任意一个中去，共有k种加入其中的方法，这样对于an的每一种加入方式，都可以使集合划分为k个子集，因此根据乘法原理，划分数共有k*S(n-1, k)个。
    综合上述的两种情况，应用加法原理，得到将n个元素的a1, a2, ···, an的集合S划分为k个子集合的划分数为以下的递归公式
    S(n, k) = S(n – 1, k – 1) + k * S(n – 1, k)（n > k, k > 0）。
    边界条件
  • 首先不能把n个元素不放入任何一个集合中去，即k=0时S(n, 0)=0；
  • 其次不可能在不允许空盒的情况下把n个元素放入多于n的k个集合中去，即k>n时，S(n, k) = 0；
  • 最后把个元素放入一个集合或者把n个元素放入n个集合中方案数都为1，即k = 1或k = n时，S(n, k) = 1。

因此，划分数S(n, k)的递归关系式为：
S(n, k) = S(n – 1, k – 1) + k * S(n – 1, k) (n > k, k > 0);
S(n, k) = 0 (n < k或k = 0);
S(n, k) = 0 (k = 1或k = n)。

编程计算 #

#include &lt; iostream &gt;
using namespace std;

int s(int n, int k){
   if(n &lt; k || k == 0) return 0;
   if(n == k || k == 1) return 1;
   return s(n - 1, k - 1) + k * s(n - 1, k);
}

int main(){
   int n, k;
   cin &gt;&gt; n &gt;&gt; k;
   cout &lt;&lt; s(n, k) &lt;&lt; endl;
   return 0;
}

分解因数 #

问题描述
给出一个正整数a，要求分解成若干个正整数的乘积，即a = a1 * a2 * a3 * … * an，并且1 < a1 <= a2 <= a3 <= … <= an，问这样的分解的种数有多少。注意到a = a也是一种分解。
输入
第1行是测试数据的组数n，后面跟着n行输入。每组测试数据占1行，包括一个正整数a (1 < a < 32768)。
输出
n行，每行输出对应一个输入。输出应是一个正整数，指明满足要求的分解的种数。
样例输入
2
2
20
样例输出
1
4

算法分析 #

令i = 2~an,通过an%i ==0来判断i是不是an的因数，如果是，则由an/i作为参数进一步带入函数来判断直至an/i == i，(此时i为最后一个因数)。
首先需知道f(m,n)的含义——求n中从m开始到n/m所有分解种数的和。而为什么每次只要满足上面的条件就算加一种情况呢？这不妨举个例子当n = 100时，2、50算一种情况，而50可以继续分为2、25，这就有了2、2、25，再继续分，且每次分都能成为其一种分解情况所以a++。

参考程序 #

#include < iostream >

using namespace std;
int s = 0;      //s用来记录分解的种类的数
void f(int x, int y)  //x为因数，y为被分解数
{
	for (int i = x; i * i >= y; ++i) {//依次试每一次分解
		if (y % i == 0) {
			++s;//种数加一
			f(i, y / i);//返回下一次函数调用
		}
	}
}
int main()
{
	int t;
	cin >> t; //输入样例的总数
	while (t--) {
		int a = 0; 
		cin >> a;
		s = 1;//a=a也算一种分解
		f(2, a);
		cout << s << endl;
	}
	return 0;
}

放苹果问题 #

问题描述
把M个同样的苹果放在N个同样的盘子里，允许有的盘子空着不放，问共有多少种不同的分法？5，1，1和1，5，1 是同一种分法。
输入
第一行是测试数据的数目t（0 <= t <= 20）。以下每行均包含二个整数M和N，以空格分开。1<=M，N<=10。
输出
对输入的每组数据M和N，用一行输出相应的K。
样例输入
1
7 3
样例输出
8

算法分析 #

该题目主要运用了递推的思维方式，解决的关键在于找出递推关系和递推出口。
m个苹果放在n个盘子中，设递推函数为apple(m,n)：
情况1：
m=0，没有一个苹果，则apple(0,n)=1；
情况2：
n=1，只有一个盘子，则apple(m,1)=1
情况3：
n>m，与m个苹果放在m个盘子中情况一样，则apple(m,n)=m
情况4：
n<=m，按是否有空盘子，又可以分为两种情况：

  • 不是所有盘子都有苹果（至少有一个盘子没有苹果），则apple(m,n-1)
  • 所有盘子都有苹果（至少每个盘子都有一个苹果），m个苹果中有n个放在n个盘子里，剩下m-n个苹果，这种情况和m-n个苹果放在n个盘子中是一样的，即apple（m-n,n）

则有以下递推关系：apple（m,n）=apple（m−n,n）+apple（m,n−1）
综上所述：可以将情况1和情况2视为一种临界条件，即为n=1时，所有苹果都在一个盘子中；m=0时，没有苹果可放！这种临界条件通常可以视为递归出口。

参考程序 #

#include < iostream >
using namespace std;
int apple(int m,int n) {
   //情况1和情况2
    if(m<=1||n==1)        return 1; 
   //情况3
    if(n>m) 
        return apple(m,m);  
    else 
        return(apple(m-n,n)+apple(m,n-1)); //情况4
}
int main() {
   //设置两个数组分别存苹果数和盘子数
    int n,a[20],b[20],i; 
    cin>>n;   
    for(i=0;i < n;i++) 
        cin>>a[i]>>b[i];  
    for(i=0;i < n;i++)   {
          cout << apple(a[i],b[i]) << endl;
      } 
    return 0;
}
您的感觉是什么