CSP-J 041 队列 – 大师码

5 min read

1. 队列概述 #

队列的基本概念 #

队列用来存储逻辑关系为“一对一”的数据，是一种“特殊”的线性存储结构。
和顺序表、链表相比，队列的特殊性体现在以下两个方面：
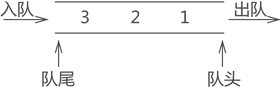
1、元素只能从队列的一端进入，从另一端出去，如下图所示：

通常，我们将元素进入队列的一端称为“队尾”，进入队列的过程称为“入队”；将元素从队列中出去的一端称为“队头”，出队列的过程称为“出队”。
2、队列中各个元素的进出必须遵循“先进先出”的原则，即最先入队的元素必须最先出队。
以上图所示的队列为例，从各个元素在队列中的存储状态不难判定，元素 1 最先入队，然后是元素 2 入队，最后是元素 3 入队。如果此时想将元素 3 出队，根据“先进先出”原则，必须先将元素 1 和 2 依次出队，最后才能轮到元素 3 出队。
强调：栈和队列不要混淆，栈是一端开口、另一端封口，元素入栈和出栈遵循“先进后出”原则；队列是两端都开口，但元素只能从一端进，从另一端出，且进出队列遵循“先进先出”的原则。

队列的实际应用 #

队列在操作系统中应用的十分广泛，比如用它解决 CPU 资源的竞争问题。

对于一台计算机来说，CPU 通常只有 1 个，是非常重要的资源。如果在很短的时间内，有多个程序向操作系统申请使用 CPU，就会出现竞争 CPU 资源的现象。不同的操作系统，解决这一问题的方法是不一样的，有一种方法就用到了队列这种存储结构。

假设在某段时间里，有 A、B、C 三个程序向操作系统申请 CPU 资源，操作系统会根据它们的申请次序，将它们排成一个队列。根据“先进先出”原则，最先进队列的程序出队列，并获得 CPU 的使用权。待该程序执行完或者使用 CPU 一段时间后，操作系统会将 CPU 资源分配给下一个出队的程序，以此类推。如果该程序在获得 CPU 资源的时间段内没有执行完，则只能重新入队，等待操作系统再次将 CPU 资源分配给它。

队列还可以用来解决一些实际问题，比如实现一个简单的停车场管理系统、实现一个推小车卡牌游戏等，后续会做详细讲解。

队列的两种实现方式 #

和栈的实现方案一样，队列的实现也有两种方式，分别是：

顺序队列：用顺序表模拟实现队列存储结构；
链队列：用链表模拟实现队列存储结构。

两者的区别仅是顺序表和链表的区别，即顺序队列集中存储数据，而链队列分散存储数据，元素之间的逻辑关系靠指针维系。

2. 顺序队列 #

顺序队列的基本实现 #

顺序队列指的是用顺序表模拟实现的队列存储结构。
我们知道，队列具有以下两个特点：

数据从队列的一端进，从另一端出；
数据的入队和出队遵循”先进先出”的原则；

在顺序表的基础上，只要元素进出的过程遵循以上两个规则，就能实现队列结构。
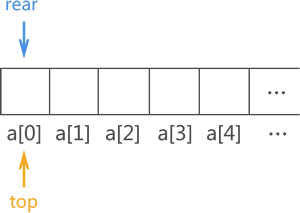
通常情况下，我们采用 C 语言中的数组实现顺序表。既然用顺序表模拟实现队列，必然要先定义一个足够大的数组。不仅如此，为了遵守队列中数据从 “队尾进，队头出” 且 “先进先出” 的规则，还需要定义两个变量（top 和 rear）分别记录队头和队尾的具体位置，如下图所示：

初始状态下，顺序队列中没有任何元素，因此 top 和 rear 重合，都位于 a[0] 处。

入队和出队 #

实现入队
当有新元素入队时，依次执行以下两步操作：

将新元素存储在 rear 记录的位置；
更新 rear 的值（rear+1），记录下一个空闲空间的位置，为下一个新元素入队做好准备。

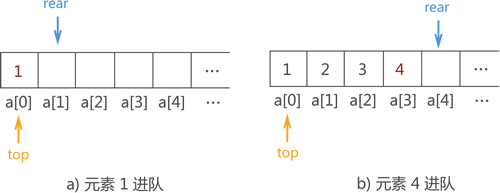
例如，上图基础上将 {1,2,3,4} 用顺序队列存储的实现操作如下所示：

入队操作的 C 语言实现代码如下：

int enQueue(int* a, int rear, int data) {
    //如果 rear 超出数组下标范围，队列将无法继续添加元素
    if (rear == MAX_LEN) {
        printf("队列已满，添加元素失败\n");
        return rear;
    }
    a[rear] = data;
    rear++;
    return rear;
}

实现出队
当有元素出队时，根据“先进先出”的原则，目标元素以及在它之前入队的元素要依次从队头出队。
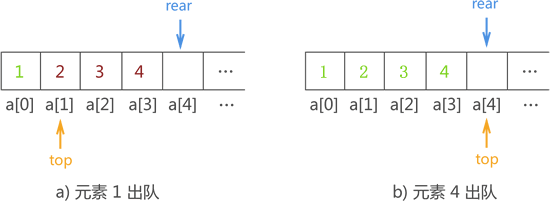
出队操作的实现方法很简单，就是更新 top 的值（top+1）。例如，在上图基础上，顺序队列中元素逐个队列的过程如下图所示：

注意，虽然数组中仍保存着 1、2、3、4 这些元素，但队列中的元素是依靠 top 和 rear 来判别的，因此图b) 显示的队列中确实不存在任何元素。
出队操作的 C 语言实现代码为：

int deQueue(int* a, int top, int rear) {
    //如果 top==rear，表示队列为空
    if (top== rear) {
        printf("队列已空，出队执行失败\n");
        return top;
    }
    printf("出队元素：%d\n", a[top]);
    top++;
    return top;
}

参考代码 #

#include<stdio.h>
#define MAX_LEN 100 //规定数组的长度
//实现入队操作
int enQueue(int* a, int rear, int data) {
    //如果 rear 超出数组下标范围，队列将无法继续添加元素
    if (rear == MAX_LEN) {
        printf("队列已满，添加元素失败\n");
        return rear;
    }
    a[rear] = data;
    rear++;
    return rear;
}
//实现出队操作
int deQueue(int* a, int top, int rear) {
    //如果 top==rear，表示队列为空
    if (top == rear) {
        printf("队列已空，出队执行失败\n");
        return top;
    }
    printf("出队元素：%d\n", a[top]);
    top++;
    return top;
}
int main() {
    int a[MAX_LEN];
    int top, rear;
    //设置队头指针和队尾指针，当队列中没有元素时，队头和队尾指向同一块地址
    top = rear = 0;
    //入队
    rear = enQueue(a, rear, 1);
    rear = enQueue(a, rear, 2);
    rear = enQueue(a, rear, 3);
    rear = enQueue(a, rear, 4);
    //出队
    top = deQueue(a, top, rear);
    top = deQueue(a, top, rear);
    top = deQueue(a, top, rear);
    top = deQueue(a, top, rear);
    top = deQueue(a, top, rear);
    return 0;
}

3. 链式队列 #

链式队列的基本实现 #

链式队列，简称”链队列”，即使用链表实现的队列存储结构。
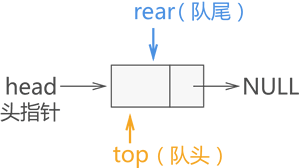
链式队列的实现思想同顺序队列类似，创建两个指针（命名为 top 和 rear）分别指向链表中队列的队头元素和队尾元素，如下图所示：

上图所示为链式队列的初始状态，此时队列中没有存储任何数据元素，因此 top 和 rear 指针都同时指向头节点。
在创建链式队列时，强烈建议初学者创建一个带有头节点的链表，这样实现链式队列会更简单。
由此，我们可以编写出创建链式队列的 C 语言实现代码为：

//链表中的节点结构
typedef struct qnode{
    int data;
    struct qnode * next;
}QNode;
//创建链式队列的函数
QNode * initQueue(){
    //创建一个头节点
    QNode * queue=(QNode*)malloc(sizeof(QNode));
    //对头节点进行初始化
    queue->next=NULL;
    return queue;
}

入队和出队 #

链式队列数据入队
链队队列中，当有新的数据元素入队，只需进行以下 3 步操作：

将该数据元素用节点包裹，例如新节点名称为 elem；
与 rear 指针指向的节点建立逻辑关系，即执行 rear->next=elem；
最后移动 rear 指针指向该新节点，即 rear=elem；

由此，新节点就入队成功了。
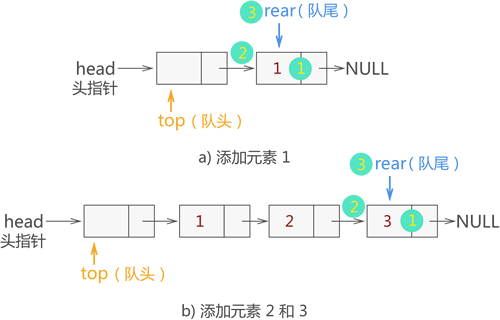
例如，在上图的基础上，我们依次将 {1,2,3} 依次入队，各个数据元素入队的过程如下图所示：

我们将链表的头部作为队列的队头，将链表的尾部作为队列的队尾。当然，也可以反过来，将链表的头部（尾部）作为队列的队尾（队头），两种存储方式都可以。
数据元素入链式队列的 C 语言实现代码为：

QNode* enQueue(QNode * rear,int data){
    //1、用节点包裹入队元素
    QNode * enElem=(QNode*)malloc(sizeof(QNode));
    enElem->data=data;
    enElem->next=NULL;
    //2、新节点与rear节点建立逻辑关系
    rear->next=enElem;
    //3、rear指向新节点
    rear=enElem;
    //返回新的rear，为后续新元素入队做准备
    return rear;
}

链式队列数据出队
当链式队列中有元素需要出队时，按照 “先进先出” 的原则，需要先将在它之前入队的元素依次出队，然后该目标元素才能出队。
我们知道，队列中的元素只能从队头出队。在图 2 中，队列的队头位于链表的头部。因此队列中元素出队的过程，其实是链表中摘除首元结点的过程，需要做以下 3 步操作：

通过 top 指针直接找到队头节点，创建一个新指针 p 指向此即将出队的节点；
将 top 所指结点的 next 指针，指向 p 结点的直接后继结点；
释放节点 p 占用的内存空间；

例如，在图b)的基础上，我们将元素 1 和 2 出队，则操作过程下图所示：

链式队列中队头元素出队的 C 语言实现代码为：

QNode* DeQueue(QNode* top, QNode* rear) {
    QNode* p = NULL;
    if (top->next == NULL) {
        printf("\n队列为空\n");
        return rear;
    }
    // 1、创建新指针 p 指向目标结点
    p = top->next;
    printf("%d ", p->data);
    //2、将目标结点从链表上摘除
    top->next = p->next;
    if (rear == p) {
        rear = top;
    }
    //3、释放结点 p 占用的内存
    free(p);
    return rear;
}

将队头元素做出队操作时，需提前判断队列中是否还有元素，如果没有，要提示用户无法做出队操作，保证程序的健壮性。此外，程序中要判断被摘除的目标结点是否是 rear 队头队尾，如果是的话，要及时更新 rear 指针的指向。

参考代码 #

这里给出链式队列入队和出队的完整 C 语言代码为：

#include<stdio.h>
#include<stdlib.h>
//链表中的节点结构
typedef struct qnode {
    int data;
    struct qnode* next;
}QNode;
//创建链式队列的函数
QNode* initQueue() {
    //创建一个头节点
    QNode* queue = (QNode*)malloc(sizeof(QNode));
    //对头节点进行初始化
    queue->next = NULL;
    return queue;
}

QNode* enQueue(QNode* rear, int data) {
    //1、用节点包裹入队元素
    QNode* enElem = (QNode*)malloc(sizeof(QNode));
    enElem->data = data;
    enElem->next = NULL;
    //2、新节点与rear节点建立逻辑关系
    rear->next = enElem;
    //3、rear指向新节点
    rear = enElem;
    //返回新的rear，为后续新元素入队做准备
    return rear;
}

QNode* deQueue(QNode* top, QNode* rear) {
    QNode* p = NULL;
    if (top->next == NULL) {
        printf("\n队列为空\n");
        return rear;
    }
    // 1、创建新指针 p 指向目标结点
    p = top->next;
    printf("%d ", p->data);
    //2、将目标结点从链表上摘除
    top->next = p->next;
    if (rear == p) {
        rear = top;
    }
    //3、释放结点 p 占用的内存
    free(p);
    return rear;
}

int main() {
    QNode* queue = NULL, * top = NULL, * rear = NULL;
    queue = top = rear = initQueue();//创建头结点
    //向链队列中添加结点，使用尾插法添加的同时，队尾指针需要指向链表的最后一个元素
    rear = enQueue(rear, 1);
    rear = enQueue(rear, 2);
    rear = enQueue(rear, 3);
    rear = enQueue(rear, 4);
    //入队完成，所有数据元素开始出队列
    rear = deQueue(top, rear);
    rear = deQueue(top, rear);
    rear = deQueue(top, rear);
    rear = deQueue(top, rear);
    rear = deQueue(top, rear);
    return 0;
}

4. 循环队列（选学） #

基本概念 #

前面讲到队列的时候提到，顺序队列的实现方案并不完美，存在一下两个弊端：

随着元素的入队和出队，队列整体向顺序表的尾部移动，队列左侧闲暇空间无法再次利用；
当队列移动到顺序表的尾部时，新元素无法入队。

采用循环队列可以彻底消除以上两个弊端。所谓循环队列，本质上使用顺序表模拟实现队列，只不过，在具体实现的过程中，会将顺序表想象成首尾相连的换装表来使用。
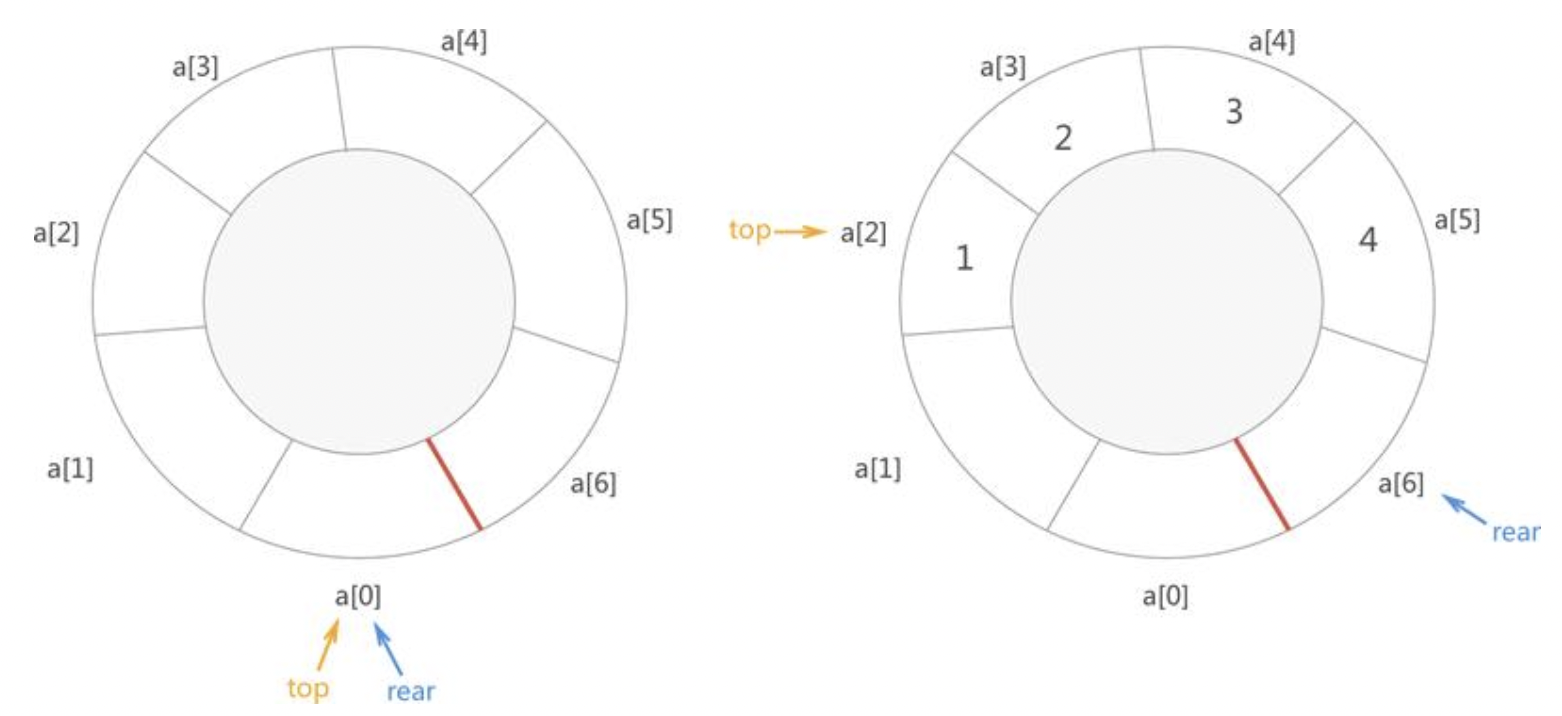
例如，下图左侧为一个空的“环状”顺序表，用它来模拟实现队列，队头（top）和队尾（rear）都位于a[0]处。下图右侧是一个存有{1,2,3,4}的循环队列，它的队头位于a[2]处，队尾位于a[6]处。

再次强调我们只是将顺序表想象成环状表来用，实际用C/C++语言程序实现循环队列时，建立的仍是普通的顺序表，后续将会讲解将循序表当作环状表使用的方法。

入队和出队 #

循环队列的入队操作
循环队列的入队操作过程和顺序队列类似，完成以下两种操作即可：

将新元素添加到rear指向的空闲空间；
rear指向下一位，指向下一个空闲空间，为下一次入队新元素做准备。

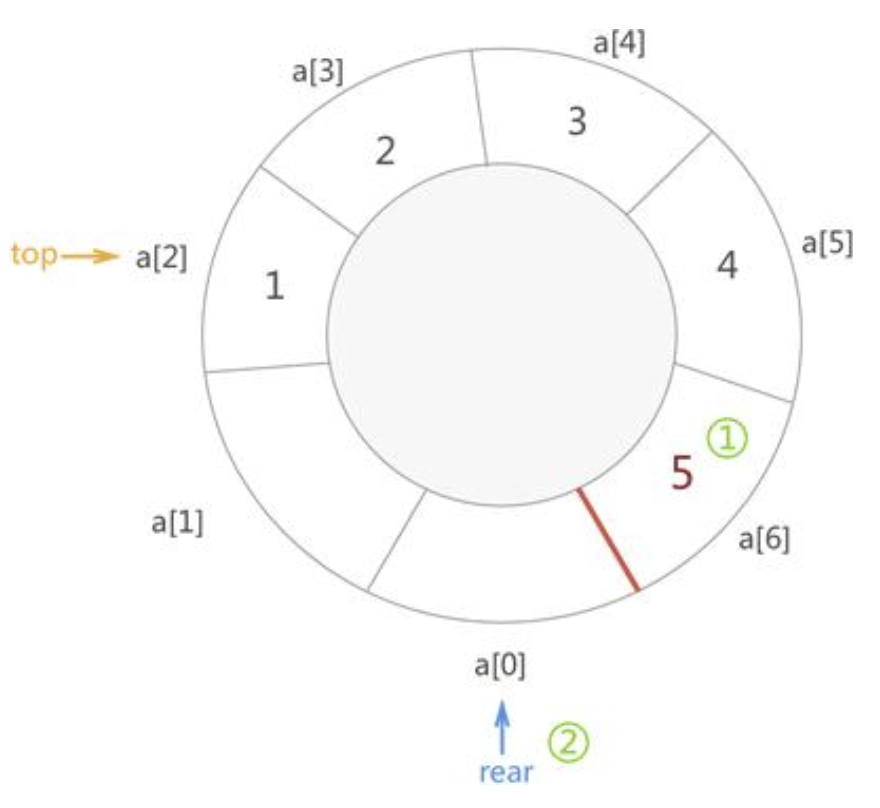
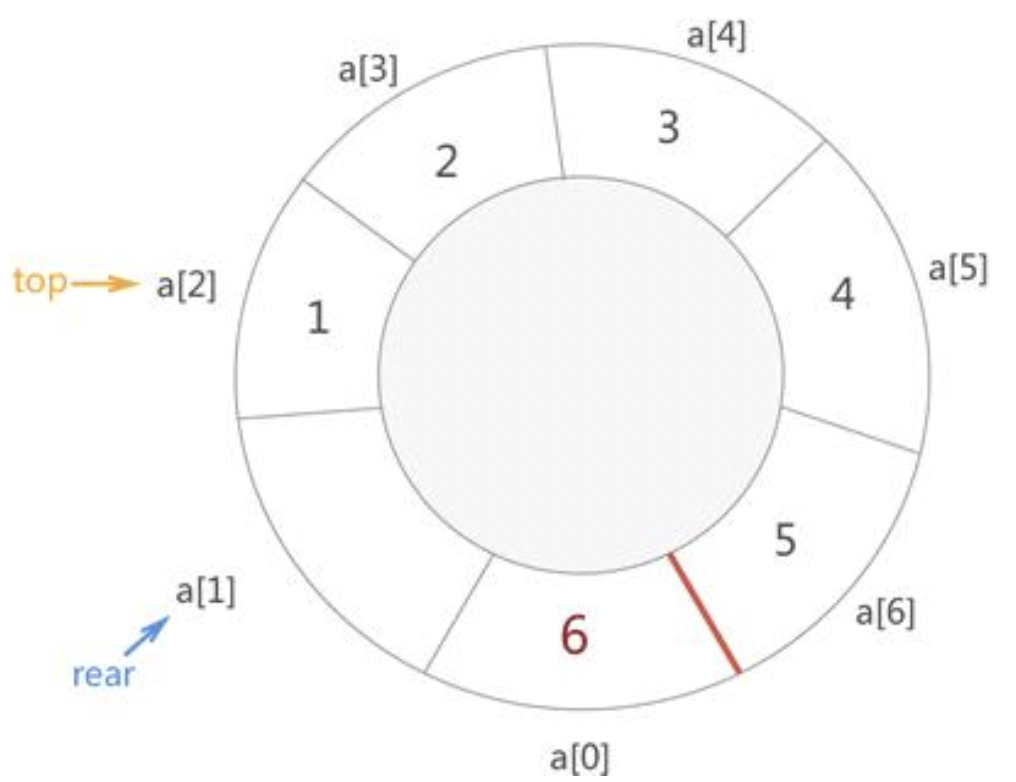
例如，在上图的基础上，向队列添加一个新元素5，实现过程如下图所示：

可以看到，当顺序表还有空间时，由于我们将它想象成“首尾相连”的状态，a[6]和a[0]挨着，rear变量会向后移一位会指向a[0]的位置。这意味着，队列左侧的空闲空间可以再次利用起来。
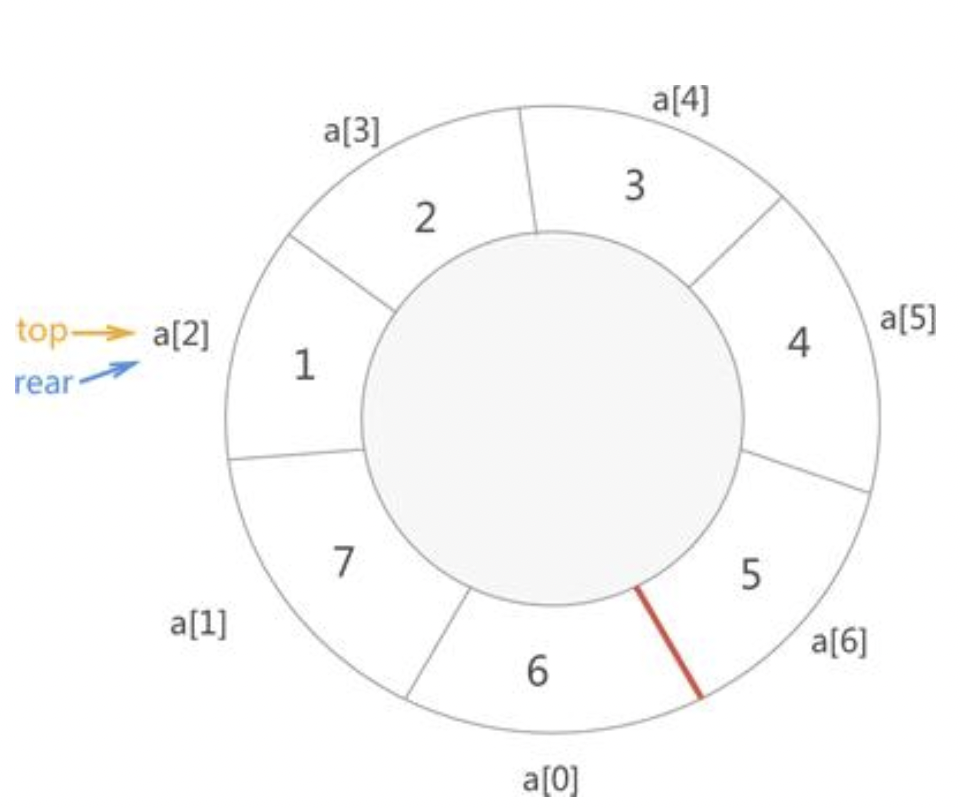
需要注意的是，循环队列判断“已满”的方式比较特殊。当我们根据上图尝试将6、7分别入队时，最终的存储状态会变成下图所示：

在第一个图中我们可以用top==rear作为空队列的判断标志，但第三张图中，队列已满的状态也是top==rear，明显它们是冲突的。解决冲突的常用方法是：仍用top==rear作为空队列的判断标志，将队列已满的判断方法改为(rear+1)%MAX_LEN==top，其中MAX_LEN为顺序表（数组）的长度。
例如，在第2张图片的基础上，尝试将元素6入队，此时rear的值为0，(rear+1)%MAX_LEN的值为1，而top的值为2，所以等式不成立，意味着队列不满，元素6就成功存储到了a[0]处。

在第4张图片的基础上，尝试将元素7入队，此时rear的值为1，(rear+1)%MAX_LEN的值为2，而top的值为2，所以等式成立，意味着循环队列已满，元素7就无法入队。
如上图所示，顺序表中明明还有一块空间没有利用呢？是的，这就是循环队列判断“已满”的方法，浪费一块存储空间，避免和“队列为空”的状态发生冲突。
循环队列实现入队的C++语言的代码如下：

int enQueue(int* a, int top, int rear, int data){
    //添加判断语句，如果rear超过max，则直接从a[0]开始存储，如果rear+1和top重合，则表示顺序表已满
    if((rear+1)%MAX_LEN == top){
        cout <<"空间已满" << endl;
        return rear;
    }
    //将新元素入队
    a[rear%MAX_LEN] = data;
    cout << "新元素" << data <<"成功入队" << endl;
    rear = (rear + 1) % MAX_LEN;
    return rear;
}

程序当中没有将data直接存储到a[rear]中，而是将其存储到a[rear%MAX_LEN]中，这样就可以将顺序表当作环表来使用。
循环队列的出队操作
循环队列的出队操作过程和顺序队列类似，完成以下两种操作即可：

将top记录的队头元素出队；
将top向后移动一位，记录新队头元素的位置。

因此循环队列实现出队操作的C++语言代码为：

int deQueue(int* a, int top, int rear){
    //如果top==rear，表示队列为空
    if(rear == top){
        cout <<"队列为空" << endl;
        return rear;
    }
    cout << "元素" << a[top]<< "成功出队" << endl;
    //top向后移动一个位置，记录新的队头
    top = (top + 1) % MAX_LEN;
    return top;
}

参考代码 #

为了加深各位同学对循环队列理解，下面给出C++实现循环队列的完成代码：

#include<iostream>
using namespace std;
#define MAX_LEN 5 //表示申请空间的大小
int enQueue(int* a, int top, int rear, int data){
    //添加判断语句，如果rear超过max，则直接从a[0]开始存储，如果rear+1和top重合，则表示顺序表已满
    if((rear+1)%MAX_LEN == top){
        cout <<"空间已满" << endl;
        return rear;
    }
    //将新元素入队
    a[rear%MAX_LEN] = data;
    cout << "新元素" << data <<"成功入队" << endl;
    rear = (rear + 1) % MAX_LEN;
    return rear;
}

int deQueue(int* a, int top, int rear){
    //如果top==rear，表示队列为空
    if(rear == top){
        cout <<"队列为空" << endl;
        return rear;
    }
    cout << "元素" << a[top]<< "成功出队" << endl;
    //top向后移动一个位置，记录新的队头
    top = (top + 1) % MAX_LEN;
    return top;
}

int main(){
    int a[MAX_LEN] = {0};
    int top = 0, rear = 0;
    rear = enQueue(a, top, rear, 1);
    rear = enQueue(a, top, rear, 2);
    rear = enQueue(a, top, rear, 3);
    rear = enQueue(a, top, rear, 4);
    //元素5入队会失败
    rear = enQueue(a, top, rear, 5);
    top = deQueue(a, top, rear);
    //元素5再入队会成功
    rear = enQueue(a, top, rear, 5);
    top = deQueue(a, top, rear);
    top = deQueue(a, top, rear);
    top = deQueue(a, top, rear);
    top = deQueue(a, top, rear);
    //队列为空时，出队操作失败
    top = deQueue(a, top, rear);
    return 0;
}

1 乐高STEAM

2 Scratch

3 Python

4 C++

5 创客

6 PPT创作

7 科创课题

8 关于我们

1. 队列概述 #

队列的基本概念 #

队列的实际应用 #

队列的两种实现方式 #

2. 顺序队列 #

顺序队列的基本实现 #

入队和出队 #

参考代码 #

3. 链式队列 #

链式队列的基本实现 #

入队和出队 #

参考代码 #

4. 循环队列（选学） #

基本概念 #

入队和出队 #

参考代码 #

您的感觉是什么

1. 队列概述 #

队列的基本概念 #

队列的实际应用 #

队列的两种实现方式 #

2. 顺序队列 #

顺序队列的基本实现 #

入队和出队 #

参考代码 #

3. 链式队列 #

链式队列的基本实现 #

入队和出队 #

参考代码 #

4. 循环队列（选学） #

基本概念 #

入队和出队 #

参考代码 #

您的感觉是什么

分享这篇文章 ：

分享这篇文章：