1. 栈概述 #
栈的基本概念 #

同顺序表和链表一样,栈也是用来存储逻辑关系为 “一对一” 数据的线性存储结构,如下图所示。
从图我们看到,栈存储结构与之前所学的线性存储结构有所差异,这缘于栈对数据 “存” 和 “取” 的过程有特殊的要求:
(1)栈只能从表的一端存取数据,另一端是封闭的。
(2)在栈中,无论是存数据还是取数据,都必须遵循”先进后出”的原则,即最先进栈的元素最后出栈。拿图 1 的栈来说,从图中数据的存储状态可判断出,元素 1 是最先进的栈。因此,当需要从栈中取出元素 1 时,根据”先进后出”的原则,需提前将元素 3 和元素 2 从栈中取出,然后才能成功取出元素 1。
因此,我们可以给栈下一个定义,即栈是一种只能从表的一端存取数据且遵循 “先进后出” 原则的线性存储结构。
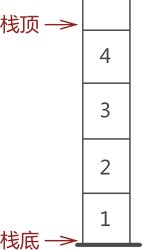
通常,栈的开口端被称为栈顶;相应地,封口端被称为栈底。因此,栈顶元素指的就是距离栈顶最近的元素,拿下图来说,栈顶元素为元素 4;同理,栈底元素指的是位于栈最底部的元素,下图中的栈底元素为元素 1。
进栈和出栈操作 #
基于栈结构的特点,在实际应用中,通常只会对栈执行以下两种操作:
- 向栈中添加元素,此过程被称为”进栈”(入栈或压栈);
- 从栈中提取出指定元素,此过程被称为”出栈”(或弹栈);
栈是一种 “特殊” 的线性存储结构,因此栈的具体实现有以下两种方式:
(1)顺序栈:采用顺序存储结构可以模拟栈存储数据的特点,从而实现栈存储结构;
(2)链栈:采用链式存储结构实现栈结构;两种实现方式的区别,仅限于数据元素在实际物理空间上存放的相对位置,顺序栈底层采用的是数组,链栈底层采用的是链表。
栈的基本应用 #
基于栈结构对数据存取采用 “先进后出” 原则的特点,它可以用于实现很多功能。
例如,我们经常使用浏览器在各种网站上查找信息。假设先浏览的页面 A,然后关闭了页面 A 跳转到页面 B,随后又关闭页面 B 跳转到了页面 C。而此时,我们如果想重新回到页面 A,有两个选择:
- 重新搜索找到页面 A;
- 使用浏览器的”回退”功能。浏览器会先回退到页面 B,而后再回退到页面 A。
浏览器 “回退” 功能的实现,底层使用的就是栈存储结构。当你关闭页面 A 时,浏览器会将页面 A 入栈;同样,当你关闭页面 B 时,浏览器也会将 B入栈。因此,当你执行回退操作时,才会首先看到的是页面 B,然后是页面 A,这是栈中数据依次出栈的效果。
不仅如此,栈存储结构还可以帮我们检测代码中的括号匹配问题。多数编程语言都会用到括号(小括号、中括号和大括号),括号的错误使用(通常是丢右括号)会导致程序编译错误,而很多开发工具中都有检测代码是否有编辑错误的功能,其中就包含检测代码中的括号匹配问题,此功能的底层实现使用的就是栈结构。
同时,栈结构还可以实现数值的进制转换功能。例如,编写程序实现从十进制数自动转换成二进制数,就可以使用栈存储结构来实现。
以上也仅是栈应用领域的冰山一角,这里不再过多举例。在后续章节的学习中,我们会大量使用到栈结构。
2. 顺序栈 #

顺序栈指的是用顺序表实现的栈存储结构,通过前面的学习我们知道,栈存储结构存取数据元素必须遵守 “先进后出” 的原则。
顺序表和栈存储数据的方式高度相似,只不过栈对数据的存取过程有特殊的限制,而顺序表没有。例如,我们使用顺序表(用 a 数组表示)存储 {1,2,3,4},存储状态如下图所示:
图1 顺序表存储 {1,2,3,4}

使用栈存储结构存储 {1,2,3,4},存储状态如下所示:
图 2 栈结构存储 {1,2,3,4}
对比上面两图不难看出,用顺序表模拟栈结构很简单,只要将数据从数组下标为 0 的位置依次存储即可。从数组下标为 0 的模拟栈存储数据是常用的方法,从其他数组下标处存储数据也完全可以,这里只是为了方便初学者理解。
栈中存取元素,必须遵循“先进后出”的原则,因此若想将图 1 中存储的元素 1 从栈中取出,需依次先将元素 4、元素 3 和元素 2 从栈中取出,最后才能取出元素 1。
这里给出一种顺序表模拟入栈和出栈的实现思路:定义一个实时记录栈顶位置的变量(假设命名为 top),初始状态下栈内无任何元素,整个栈是”空栈”,top 的值为 -1。一旦有数据元素进栈,则 top 就做 +1 操作;反之,如果数据元素出栈,top 就做 -1 操作。
顺序栈元素入栈 #

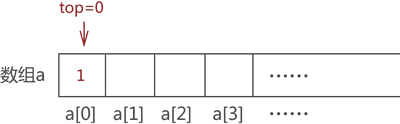
比如,还是模拟栈存储 {1,2,3,4} 的过程。最初栈是”空栈”,top 的值为 -1,如图 3 所示:
图 3 空栈示意图
将元素 1 入栈,默认数组下标为 0 一端表示栈底,元素 1 存储在数组 a[0] 处,同时 top 值 +1,如图 4 所示:
图 4 模拟栈存储元素 1
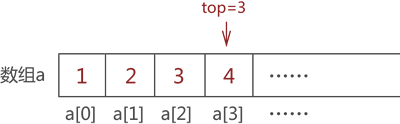
采用同样的方式,依次将元素 2、3 和 4 入栈,最终 top 的值变成 3,如图 5 所示:
图 5 模拟栈存储{1,2,3,4}
因此,C++语言实现代码为:
//元素elem进栈,a为数组,top值为当前栈的栈顶位置
int push(int* a,int top,int elem){
a[++top]=elem;
return top;
}
代码中的 a[++top]=elem,等价于先执行 ++top,再执行 a[top]=elem。
顺序栈元素出栈 #
实际上,top 变量的设置对模拟数据的 “入栈” 操作没有帮助,它是为实现数据的 “出栈” 操作做准备的。
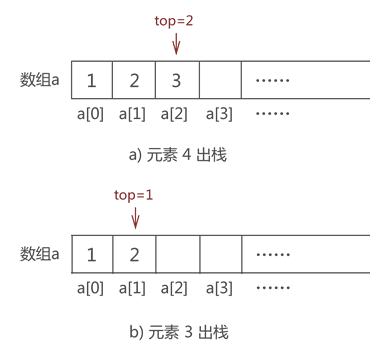
比如,将图 5 中的元素 2 出栈,则需要先将元素 4 和元素 3 依次出栈。需要注意的是,当有数据出栈时,要将 top 做 -1 操作。因此,元素 4 和元素 3 出栈的过程分别如图 6a) 和 6b) 所示:
图 6 数据元素出栈
元素 4 和元素 3 全部出栈后,元素 2 才能出栈。因此,使用顺序表模拟数据出栈操作的 C++语言实现代码为:
//数据元素出栈
int pop(int * a,int top){
if (top == -1) {
cout << "空栈";
return -1;
}
cout << "弹栈元素: " << a[top] << endl;
代码中的 if 语句是为了防止用户做 “栈中已无数据却还要做出栈操作” 的错误操作。细心的读者还可能发现,出栈操作只是将 top 的值减 1,并没有像图 6 那样将出栈元素从数组中手动删除。这是因为,当有新的元素入栈后,新元素会将出栈元素覆盖掉,所以不删除出栈元素,也不会影响栈的正常使用,何必多此一举。
参考代码 #
这里给出顺序栈及对数据基本操作的 C++语言完整代码:
#include <iostream>
using namespace std;
//元素elem进栈
int push(int* a, int top, int elem) {
a[++top] = elem;
return top;
}
//数据元素出栈
int pop(int* a, int top) {
if (top == -1) {
cout << "空栈";
return -1;
}
cout << "弹栈元素:" << a[top] << endl;
top--;
return top;
}
int main() {
int a[100];
int top = -1;
top = push(a, top, 1);
top = push(a, top, 2);
top = push(a, top, 3);
top = push(a, top, 4);
top = pop(a, top);
top = pop(a, top);
top = pop(a, top);
top = pop(a, top);
top = pop(a, top);
return 0;
}
3. 链栈 #

链栈是栈的一种实现方法,特指用链表实现栈存储结构。
链栈的实现思路和顺序栈类似,顺序栈是将顺序表(数组)的一端做栈底,另一端做栈顶;链栈也是如此,我们通常将链表的头部做栈顶,尾部做栈底,如图 1 所示:
图 1 链栈示意图
以链表的头部做栈顶,最大的好处是:可以避免在实现元素 “入栈” 和 “出栈” 时做大量遍历链表的耗时操作。有元素入栈时,只需要将其插入到链表的头部;有元素出栈时,只需要从链表的头部依次摘取结点。
因此,链栈实际上是一个采用头插法插入或删除数据的链表。
链栈元素入栈 #

例如,依次将 1、2、3、4 存储到栈中,每个元素的入栈过程如图 2 所示:
图 2 链栈元素依次入栈过程示意图
C++语言实现代码为:
//链表中的节点结构
struct LineStack {
int data;
struct LineStack* next;
};
//stack为当前的链栈,a表示入栈元素
LineStack* push(LineStack* stack, int a) {
//创建存储新元素的节点
LineStack* line = (LineStack*)malloc(sizeof(LineStack));
line->data = a;
//新节点与头节点建立逻辑关系
line->next = stack;
//更新头指针的指向
stack = line;
return stack;
}
链栈元素出栈 #
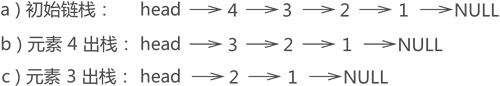
在图 2e) 所示链表的基础上,假设将元素 3 从栈中取出,根据”先进后出”的原则,要先将元素 4 出栈,然后元素 3 才能出栈,整个操作过程如图 3 所示:
图 3 链栈元素出栈示意图
实现栈顶元素出栈的C++语言代码为:
//栈顶元素出链栈的实现函数
LineStack* pop(LineStack* stack) {
if (stack) {
//声明一个新指针指向栈顶节点
LineStack* p = stack;
//更新头指针
stack = stack->next;
cout <<"出栈元素: " << p->data ;
if (stack) {
cout << "新栈顶元素 " << stack->data << endl;
}
else {
cout << "栈已空" << endl;;
}
free(p);
}
else {
cout << "栈内没有元素";
return stack;
}
return stack;
}
代码中通过使用 if 判断语句,避免了用户执行”栈已空却还要数据出栈”错误操作。
参考代码 #
这里给出链栈及基本操作的C++语言完整代码:
#include <iostream>
using namespace std;
//链表中的节点结构
struct LineStack {
int data;
struct LineStack* next;
};
//stack为当前的链栈,a表示入栈元素
LineStack* push(LineStack* stack, int a) {
//创建存储新元素的节点
LineStack* line = (LineStack*)malloc(sizeof(LineStack));
line->data = a;
//新节点与头节点建立逻辑关系
line->next = stack;
//更新头指针的指向
stack = line;
return stack;
}
//栈顶元素出链栈的实现函数
LineStack* pop(LineStack* stack) {
if (stack) {
//声明一个新指针指向栈顶节点
LineStack* p = stack;
//更新头指针
stack = stack->next;
cout <<"出栈元素: " << p->data ;
if (stack) {
cout << "新栈顶元素 " << stack->data << endl;
}
else {
cout << "栈已空" << endl;;
}
free(p);
}
else {
cout << "栈内没有元素";
return stack;
}
return stack;
}
int main() {
LineStack* stack = NULL;
stack = push(stack, 1);
stack = push(stack, 2);
stack = push(stack, 3);
stack = push(stack, 4);
stack = pop(stack);
stack = pop(stack);
stack = pop(stack);
stack = pop(stack);
stack = pop(stack);
return 0;
}
程序运行结果为:
弹栈元素:4 栈顶元素:3 弹栈元素:3 栈顶元素:2 弹栈元素:2 栈顶元素:1 弹栈元素:1 栈已空 栈内没有元素
4. 栈的应用:括号匹配 #
问题描述 #
假设一个表达式有英文字母(小写)、运算符(+,—,∗,/)和左右小(圆)括号构成,以“@”作为表达式的结束符。请编写一个程序检查表达式中的左右圆括号是否匹配,若匹配,则返回“YES”;否则返回“NO”。表达式长度小于255,左圆括号少于20个。
输入描述
一行数据,即表达式。
输出描述
一行,即“YES” 或“NO”。
输入样例
2*(x+y)/(1-x)@
输出样例
YES
问题分析 #
假设输入的字符串存储在一个C风格的字符串中(char str[255])。
我们可以定义一个栈:char str[256],用它来存放从左到右的括号。
自左向右地逐个考查 str 中每个字符,如果遇到左括号,则将该括号入栈,如果遇到右括号,则将其与栈顶的括号比对,如果能正好凑成一对括号,则将栈顶的括号出栈,继续考查str中的下一个字符。如果不能正好凑成一对括号,则该str中的括号一定是不匹配的。如果str中所有字符都考察完了,而栈不为空,str中的括号也是不匹配的。
参考程序 #
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
int main()
{
char str[255];
cin >>str;
int i=0,top=0;
cout << 3 << endl;
while(str[i]!='@')
{
if(str[i]=='(') top++; //表示左括号的数量
if(str[i]==')')
{
if(top>=0) top--; //遇到匹配的括号则将相应的左括号弹出
else break; //右括号数目多于左括号数目
}
i++;
}
if(top!=0) cout<<"NO";
else cout<<"YES";
}
5. 栈的应用:后缀表达式求值 #
后缀表达式 #
所谓表达式,就是由变量、常量以及运算符组合而成的式子。其中,常用的运算符无非 !(阶乘运算符)、^(指数 运算符)、+、-、*、/ 、( ) 这几种,比如 3!+4*2/(1-5)^2 就是一个表达式。
那么,如何用栈结构求一个表达式的值呢?实际上,已经有前辈设计好了一种完美的解决方案。
1929 年,波兰逻辑学家 J・卢卡西维兹提出了一种全新的表示表达式的方法,称为后缀表达式或者逆波兰表达式。 和普通表达式不同,后缀表达式习惯将运算符写在它的运算项之后,且整个表达式中不用括号 () 表明运算的优先
级关系。
以 3! 为例,! 为运算符,3 为运算项,因此 3! 本身就是一个后缀表达式;再以 4*2 为例,* 为运算符,4 和 2 作为它的运算项,其对应的后缀表达式为 4 2+。
在此基础上,我们试着将 3!+4*2/(1-5)^2 转换成后缀表达式,其过程也就是将表达式中所有运算符放置在它的运 算项之后:
- ! 运算符对应的运算项为 3,转换后得到 3 !;
- + 运算符对应的运算项是 3! 和 4*2/(1-5)^2,转换之后得到:3! 4*2/(1-5)^2 +;
- * 运算符对应的运算项是 4 和 2,转换之后得到 4 2 *;
- / 运算符对应的运算项是 4 2 * 和 (1-5)^2,转换后得到 4 2 * (1-5)^2 /;
- – 运算符对应的运算项是 1 和 5,转换后得到 1 5 -;
- ^ 运算符对应的运算项是 15- 和 2 ,转换后得到15-2^。
整合之后,整个普通表达式就转换成了 3 ! 4 2 * 1 5 – 2 ^ / +,这就是其对应的后缀表达式。
问题分析 #
不难发现,后缀表达式完全舍弃了表达式应有的可读性,但有失必有得,相比于普通的表达式,后缀表达式的值可以轻松借助栈存储结构求得。具体求值过程为:当用户给定一个后缀表达式时,按照从左到右的顺序依次扫描表达式中的各个运算项和运算符,对它们进行如下处理:
- 遇到运算项时直接入栈;
- 遇到运算符时,将位于栈顶的运算项出栈,对于!运算符,取栈顶一个运算项;其他运算符,取栈顶两个运算项,第一个取出的运算项作为该运算符的右运算项,另一个作为左运算项。求此表达式的的值并将其入栈。
经过以上操作,知道栈中仅存在一个运算项为止,此运算项即为整个表达式的值。
举例说明 #
以3!4 2*1 5-2^/+表达式为例,求值过程为:
1) 从3开始,它是运算项,因此直接入栈:

2) !作为运算符,从栈顶取1个运算项(也就是3),求3!的值(3!=3*2*1=6)并将其入栈:

3) 将4和2先后入栈:

4) 对于运算符*取两个运算项(2和4),其中先取出的2作为*的右操作数,4作为左操作数。求4*2的值8,并将其入栈:

5) 将1和5先后入栈:

6) 对于-运算符,取栈顶两个运算项(5和1),计算出1-5的值为-4,将其入栈:

7) 将2入栈:
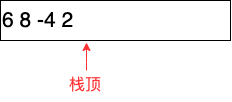
8) 对于^运算符,取栈顶2个运算项(2和-4),计算出-4^2的值16,将其入栈:
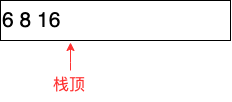
9) 对于/运算符,取栈顶2个运算项(16和8),计算出8/16的值0.5,将其入栈:

10) 对于+运算符,取栈顶2个运算项(0.5和6),计算出6+0.5的值6.5,将其入栈:

参考代码 #
由此,整个表达式的求值过程就结束了,最终表达式的值为6.5.如下给出了实现此过程的参考代码:
//根据后缀表达式posdtexp,计算它的值
#include <iostream>
using namespace std;
#define MAXSIZE 100
class Stack_num{
public:
double data[MAXSIZE];
int top;
};
void InitSrack_num(Stack_num **s){
*s = (Stack_num *) malloc(sizeof(Stack_num));
(*s) -> top = -1;
}
bool Push_num(Stack_num **s, double e){
if((*s) -> top == MAXSIZE - 1){
return false;
}
(*s) -> top++;
(*s) -> data[(*s) -> top] = e;
return true;
}
bool Pop_num(Stack_num **s, double *e){
if((*s) -> top == -1)
return false;
*e = (*s) -> data[(*s) -> top];
(*s) -> top--;
return true;
}
//计算后缀表达式的值
double compValue(char *postexp){
Stack_num *num;
int i = 1;
double result;
double a, b;
double c;
double d;
InitSrack_num(&num);
//依次扫描整个表达式
while(*postexp != '\0'){
switch (*postexp)
{
case '+':
Pop_num(&num, &a);
Pop_num(&num, &b);
//计算b+a的值
c = b + a;
Push_num(&num, c);
cout << '+' << c << endl;
break;
case '-':
Pop_num(&num, &a);
Pop_num(&num, &b);
//计算b-a的值
c = b - a;
Push_num(&num, c);
cout << '-' << c << endl;
break;
case '*':
Pop_num(&num, &a);
Pop_num(&num, &b);
//计算b*a的值
c = b * a;
Push_num(&num, c);
cout << '*' << c << endl;
break;
case '/':
Pop_num(&num, &a);
Pop_num(&num, &b);
//计算b/a的值
if(a != 0){
c = b / a;
Push_num(&num, c);
}else{
cout << "除零错误!" << endl;
exit(0);
}
cout << '/' << c << endl;
break;
case '^':
Pop_num(&num, &a);
Pop_num(&num, &b);
//计算b^a的值
if (a != 0){
i = 1;
c = 1;
while(i <= a){
c = c * b;
i++;
}
}else if(b != 0){
c = 1;
}else{
c = 0;
}
Push_num(&num, c);
cout << '^' <<c << endl;
break;
case '!':
Pop_num(&num, &a);
//计算a!的值
c = 1;
i = a;
while(i != 0){
c = c * i;
i--;
}
Push_num(&num, c);
cout << '!' << c << endl;
break;
default:
//如果不是运算符,就只能是字符形式的数字,将其转换成对应的整数
d = 0;
while(*postexp >= '0' && *postexp <= '9'){
d = 10 * d + (*postexp - '0');
postexp++;
}
Push_num(&num, c);
}
postexp++; //继续下一个字符
}
Pop_num(&num, &result);
return result;
}



