哈夫曼树介绍 #

哈夫曼树也称为最优二叉树，给定n个权值作为n个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，即为哈夫曼树

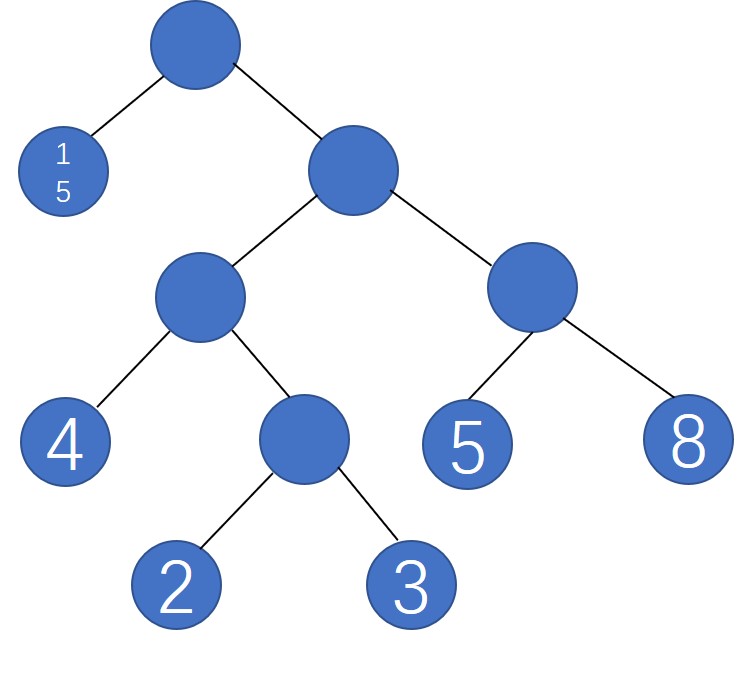
哈夫曼树中有这样几个名词需要了解：

1. 路径：在一棵树中，一个结点到另一个结点之间的通路，称为路径
2. 路径长度：在一条路径中，每经过一个结点，路径长度都要加1。例如在一棵树中，规定根结点所在层数为1层，那么从根结点到第i层结点的路径长度为i-1。上图中从根结点到结点5的路径长度为3
3. 结点的权：给每一个结点赋予一个新的数值，被称为这个结点的权，也就是每个结点的值
4. 结点的带权路径长度：指的是从根结点到该结点之间的路径长度与该结点的权的乘积。如结点5的带权路径长度为 3 * 5 = 15

哈夫曼树构建算法 #

在构建哈弗曼树时，要使树的带权路径长度最小，只需要遵循一个原则：权重越大的结点离树根越近。
可以按照下述步骤构建哈夫曼树：

1. 首先，找出所有元素中权重最小的两个元素
2. 以最小的两个元素为子结点构建二叉树，则构建的二叉树的父结点的权重为两个子结点之和
3. 剩下的元素和新构建的的父结点中选出权重最小的两个节点

进行第2步操作

以此类推，直至最后合成一个二叉树就是哈夫曼树

树的构造 #

哈夫曼树中的权即是结点的值，除外，还有左子树和右子树：

class BinaryTree:
    def __init__(self, name, weight):
        self.name = name
        self.weight = weight
        self.left = None
        self.right = None

哈夫曼树的构建 #

先获取最小的两个结点，然后构造以此两结点为子结点的树，根结点为子结点的权值和

def makeHuffman(source):
    m2, name = getMin2(source)
    print(m2[0].name, m2[1].name)
    left = m2[0]
    right = m2[1]
    sumLR = left.weight + right.weight
    father = BinaryTree(None, sumLR)
    father.left = left
    father.right = right
    if name == []:
        return father
    name.append(father)
    return makeHuffman(name)

完整实现 #

from collections import deque

class BinaryTree:
    def __init__(self, name, weight):
        self.name = name
        self.weight = weight
        self.left = None
        self.right = None
    
def getMin2(li):
    # 定义获取列表中权重最小的两个结点：
    result = [BinaryTree(None, float('inf')), BinaryTree(None, float('inf'))]
    list_new = []
    for i in range(len(li)):
        if li[i].weight < result[0].weight:
            if result[1].weight != float('inf'):
                list_new.append(result[1])
            result[0], result[1] = li[i], result[0]
        elif li[i].weight < result[1].weight:
            if result[1].weight != float('inf'):
                list_new.append(result[1])
            result[1] = li[i]
        else:
            list_new.append(li[i])
    return result, list_new
    
def makeHuffman(source):
    m2, name = getMin2(source)
    print(m2[0].name, m2[1].name)
    left = m2[0]
    right = m2[1]
    sumLR = left.weight + right.weight
    father = BinaryTree(None, sumLR)
    father.left = left
    father.right = right
    if name == []:
        return father
    name.append(father)
    return makeHuffman(name)
    
def breadthFirst(gen, index=0, nextGen=[], result=[]):
    # 遍历输出结果
    if type(gen) == BinaryTree:
        gen = [gen]
    result.append((gen[index].name, gen[index].weight))
    if gen[index].left != None:
        nextGen.append(gen[index].left)
    if gen[index].right != None:
        nextGen.append(gen[index].right)
    if index == len(gen)-1:
        if nextGen == []:
            return
        else:
            gen = nextGen
            nextGen = []
            index = 0
    else:
        index += 1
    breadthFirst(gen, index, nextGen, result)
    return result
    
sourceData = [('a', 5), ('b', 4), ('c', 3), ('d', 8),  ('f', 15), ('g', 2)]
sourceData = [BinaryTree(x[0], x[1]) for x in sourceData]
    
huffman = makeHuffman(sourceData)
print(breadthFirst(huffman))  

哈夫曼编码 #

如果将访问左节点定义为0，访问右节点定义为1，那么访问某个结点所形成的二进制码就称为哈夫曼编码。例如图中的5，对应
哈夫曼编码为110，而结点8的哈夫曼编码为111。