跳至正文
View Categories

1 min read

图的定义 #

定义：图（Graph）是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：G(V,E)，其中，G表示一个图，V是图G中顶点的集合，E是图G中边的集合。
在图中需要注意的是：

  1. 线性表中我们把数据元素叫元素，树中将数据元素叫结点，在图中数据元素，我们则称之为顶点（Vertex）。
  2. 线性表可以没有元素，称为空表；树中可以没有节点，称为空树；但是，在图中不允许没有顶点（有穷非空性）。
  3. 线性表中的各元素是线性关系，树中的各元素是层次关系，而图中各顶点的关系是用边来表示（边集可以为空）。

图的基本概念 #

（1）无向图

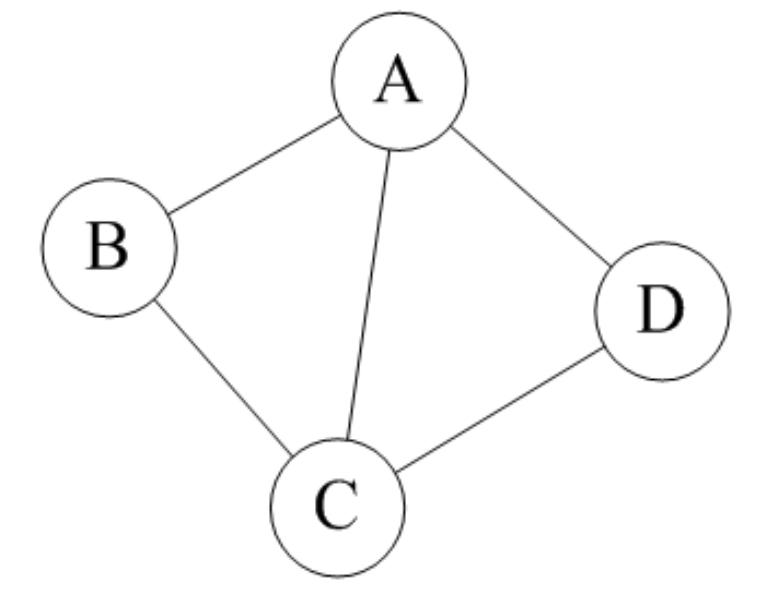
如果图中任意两个顶点之间的边都是无向边（简而言之就是没有方向的边），则称该图为无向图（Undirected graphs）。
（2）有向图

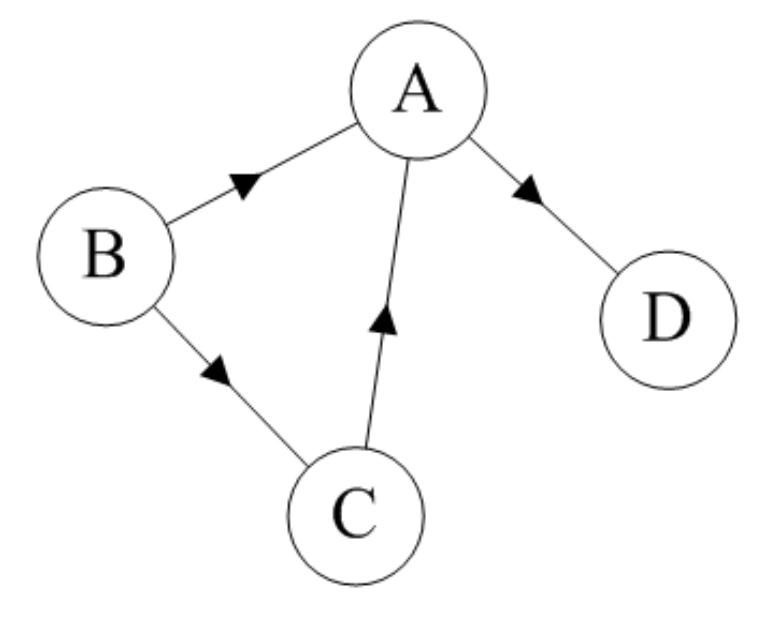
如果图中任意两个顶点之间的边都是有向边（简而言之就是有方向的边），则称该图为有向图（Directed graphs）。
（3）完全图
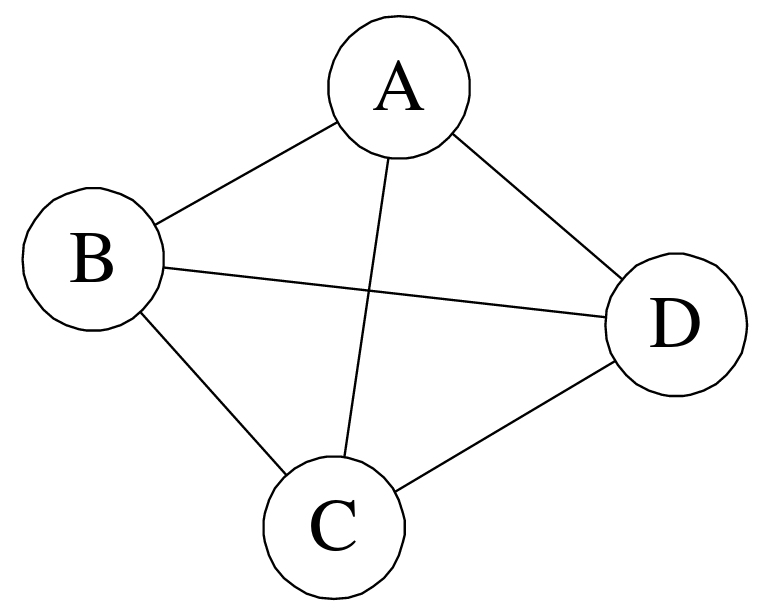
①无向完全图：在无向图中，如果任意两个顶点之间都存在边，则称该图为无向完全图。（含有n个顶点的无向完全图有(n×(n-1))/2条边）如下图所示：

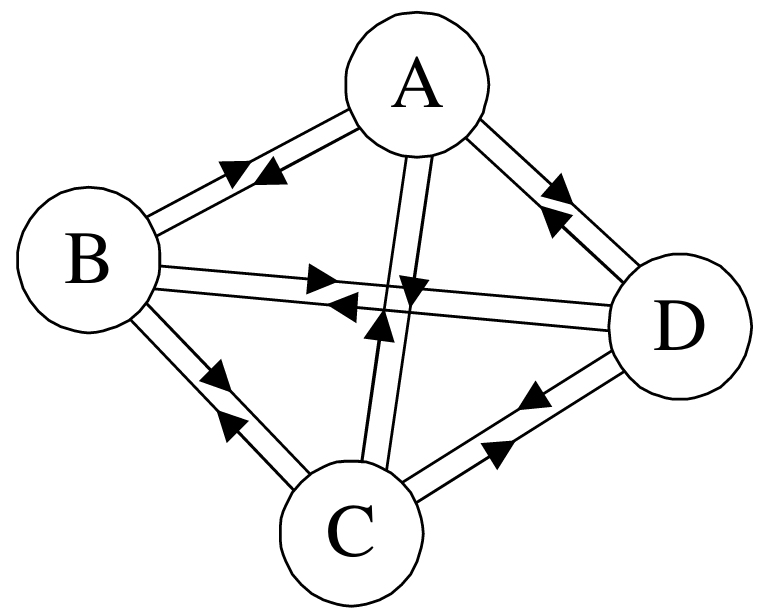
②有向完全图：在有向图中，如果任意两个顶点之间都存在方向互为相反的两条弧，则称该图为有向完全图。（含有n个顶点的有向完全图有n×(n-1)条边）如下图所示：

（4）顶点的度
顶点Vi的度是指在图中与Vi相关联的边的条数。对于有向图来说，有入度和出度之分，有向图顶点的度等于该顶点的入度和出度之和。
（5）邻接
①若无向图中的两个顶点V1和V2存在一条边(V1,V2)，则称顶点V1和V2邻接；
②若有向图中存在一条边<V3,V2>，则称顶点V3与顶点V2邻接，且是V3邻接到V2或V2邻接直V3；
无向图中的边使用小括号“()”表示，而有向图中的边使用尖括号“<>”表示。
（6）路径
在无向图中，若从顶点Vi出发有一组边可到达顶点Vj，则称顶点Vi到顶点Vj的顶点序列为从顶点Vi到顶点Vj的路径。
（7）连通
若从Vi到Vj有路径可通，则称顶点Vi和顶点Vj是连通的。
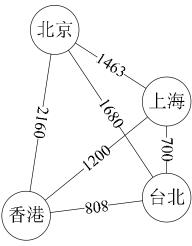
（8）权

有些图的边或弧具有与它相关的数字，这种与图的边或弧相关的数叫做权。

连通图的概念 #

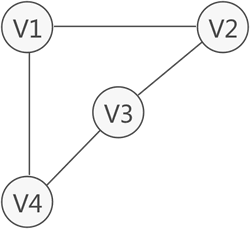
前面讲过，图中从一个顶点到达另一顶点，若存在至少一条路径，则称这两个顶点是连通着的。例如下图中，虽然 V1 和 V3 没有直接关联，但从 V1 到 V3 存在两条路径，分别是 V1-V2-V3 和 V1-V4-V3，因此称 V1 和 V3 之间是连通的。

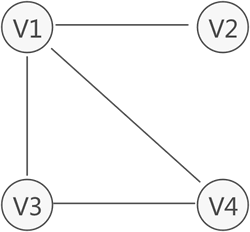
无向图中，如果任意两个顶点之间都能够连通，则称此无向图为连通图。例如，下图中的无向图就是一个连通图，因为此图中任意两顶点之间都是连通的。

图的存储结构 #

邻接矩阵存储方式简介 #

使用数组存储图时，需要使用两个数组，一个数组存放图中顶点本身的数据（一维数组），另外一个数组用于存储各顶点之间的关系（二维数组）即邻接矩阵。

存储图中各顶点本身数据，使用一维数组就足够了；存储顶点之间的关系时，要记录每个顶点和其它所有顶点之间的关系，所以需要使用二维数组。

邻接矩阵的英文名是 adjacency matrix。它的形式是 bool adj[n][n] , 这里需要存 n 个节点，adj[x][y] 表示节点x与节点y 之间是否有边，如果边有权值的话 , 用 int adj[n][n] 直接把边权存进去。

有向图需要 x 与 y 有边则需要存 adj[x][y] 与 adj[y][x] 表示有双向导通 , 无向图则 x -> y 则存 adj[x][y] 就行了 。

include<stdio.h>
 
 
int adj[MAXN][MAXN],n,m;  // n 为节点数 , m 为边数
 
int main()
{
    scanf("%d %d",&n,&m);
    for(int i=1;i<=m;i++)
    {
        int x,y,v;
        scanf("%d %d %d",&x,&y,&v);
        adj[x][y]=adj[y][x]=v;//向x,y间添加一个权值为v的边(无向)
        //有向图为adj[x][y]=v;
    }
    return 0;
}

它的优点是 , 在查询两点间是否有边时 , 时间复杂度为 O(1) , 但是缺点是它存边却是极占内存，它的空间(内存)复杂度是 O(n^2) . 对于一个稀疏的图（边相对于点数的平方比较少）来说，用邻接矩阵来存的话，成本偏高。
如果n*m超过3×1e7，内存就超过128MB了，所以当看到类似的 n,m=<1e4时就不要用邻接矩阵 , 需要考虑其他的存储方式。

邻接表存储方式简介 #

邻接表（Adjacency List）是图的一种链式存储结构，既可以存储无向图（网），也可以存储有向图（网）。

邻接表存储图的核心思想是：将图中的所有顶点存储到顺序表中（也可以是链表），同时为各个顶点配备一个单链表，用来存储和当前顶点有直接关联的边或者弧（边的一端是该顶点或者弧的弧尾是该顶点）。

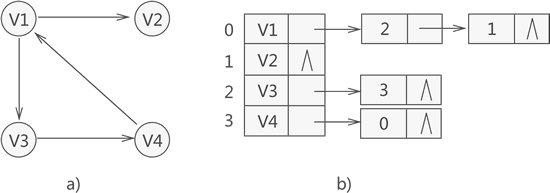
举个简单的例子，下图是一张有向图和它对应的邻接表：

#include<stdio.h>
 
struct node
{
    int to[1010];  //存储与当前节点相接的节点
    int v[1010];   //两节点间的边的权值
    int olen;      //出度
    //int ilen;      //入度 
}edge[1010];
int n,m;
int main()
{
    scanf("%d %d",&n,&m);
    for(int i=1;i<=m;i++)
    {
        int x,y,v1;
        scanf("%d %d %d",&x,&y,&v1);
        edge[x].len++;edge[y].len++;
        edge[x].to[edge[x].len]=y;edge[y].to[edge[x].len]=x;
        edge[x].v[edge[x].len]=edge[y].to[edge[x].len]=v1;//向x,y间添加一个权值为v的边(无向)
        /*有向图为
        edge[x].len++;
        edge[x].to[edge[x].len]=y;
        edge[x].v[edge[x].len]=v1;
        */
    }
    return 0;
}
What are your Feelings