概述 #

基本概念 #

贪心的本质是选择每一阶段的局部最优，从而达到全局最优。
这么说有点抽象，来举一个例子：
例如，有一堆钞票，你可以拿走十张，如果想达到最大的金额，你要怎么拿？
指定每次拿最大的，最终结果就是拿走最大数额的钱。
每次拿最大的就是局部最优，最后拿走最大数额的钱就是推出全局最优。
贪心算法没有固定的算法框架，算法设计的关键是贪心策略的选择。必须注意的是，贪心算法不会对所有问题都能得到整体最优解，选择贪心的策略必须具备无后效性，即某个状态以后的过程不回影响以前的状态，至于当前状态有关。
所以采用贪心策略一定要仔细分析其其是否满足无后效性。

基本思路 #

1. 建立数学模型来描述问题。
2. 把求解的问题分成若干的问题。
3. 对每一个字问题求解，得到子问题的局部最优解。
4. 把子问题的局部最优解合成原来的问题。

适用问题 #

贪心策略适用的前提是：局部最优策略能够导致产生全局最优解。
因为贪心算法只能通过解局部最优解的策略来达到全局最优解，因此，一定要注意判断问题是否适合采用贪心算法策略，找到的解是否一定是问题的最优解。

实现框架 #

从一个问题的某一初始解出发；
while(能够朝着总目标前进一步){
    利用可行的决策，求出一个可行解的解元素；
}
由所有解元素组合成问题的一个可行解；

例题 – 排队打水 #

问题描述 #

有n个人排队到r个水龙头去打水，他们装满水桶的时间t1、t2………..tn为整数且各不相等，应如何安排他们的打水顺序才能使他们总共花费的时间最少？
输入格式
第一行n，r (n<=500,r<=75)
第二行为n个人打水所用的时间Ti (Ti<=100)；
输出格式
最少的花费时间
样例输入
3 2
1 2 3
样例输出
7

算法思路 #

这道题最后要求
花费的时间=每个人接水的时间+每个人排队等待的时间
确定了这个就很好求了
这个题的贪心策略：
因为每个人的接水时间已经是固定的了，那么要确定最少的花费时间
就取决于让每个人排队等待的时间最少
这样让接水时间少的人先接,就能保证后面排队的人用时最短。
(1)将输入的时间按照从小到大排序；
(2)将排序后的时间按找顺序依次放入每个水龙头的队列中；
(3)统计，输出答案。

参考程序 #

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
int main()
{
    int n,r,sum=0;     //人数，水龙头数
    int s[5000],arr[5000];  //装满水桶的时间
    memset(s,0,sizeof(s));  //初始化
    cin >> n >> r;
    for(int i=1; i<=n; i++)
        cin >> arr[i];
    sort(arr+1,arr+1+n);  //从小到大排序
    int k=0;
    for(int i=1;i<=n;i++)
    {
        k++;
        if(k==r+1) //r人一组,第r+1个人回到第一个龙头
            k=1;
        s[k] += arr[i];//加上等待时间
        sum += s[k];//累加
    }
    cout << sum << endl;
    return 0;
}

例题 – 均分纸牌 #

问题描述 #

有 N 堆纸牌，编号分别为 1，2，…, N。每堆上有若干张，但纸牌总数必为 N 的倍数。可以在任一堆上取若干张纸牌，然后移动。
移牌规则为：在编号为 1 堆上取的纸牌，只能移到编号为 2 的堆上；在编号为 N 的堆上取的纸牌，只能移到编号为 N-1 的堆上；其他堆上取的纸牌，可以移到相邻左边或右边的堆上。
现在要求找出一种移动方法，用最少的移动次数使每堆上纸牌数都一样多。例如 N=4，4 堆纸牌数分别为： ①　9　②　8　③　17　④　6
移动3次可达到目的：
从 ③ 取4张牌放到④（9 8 13 10）->从③取3张牌放到 ②（9 1110 10）-> 从②取1张牌放到①（10 10 10 10）。
输入格式
N（N 堆纸牌，1 <= N <=100）
A1 A2 … An （N 堆纸牌，每堆纸牌初始数，l<= Ai <=10000）
输出格式
所有堆均达到相等时的最少移动次数。
样例输入
4
9 8 17 6
样例输出
3

算法思路 #

以正常人的思维来想，肯定是从纸牌数最多的牌堆开始往旁边的牌堆移动纸牌，但是如果要程序中模拟这个过程无疑是比较困难的。因为是计算机处理的缘故，我们可以移动负数张纸牌，且最后达到的效果一样。
一开始先求出牌数的平均值，然后从第1堆开始遍历到第n-1堆牌，如果堆中的牌数不等于平均值，就移动堆中的牌数与平均值的差值张牌（这里无论正负）。接着，下一堆接收到移动过来的牌后，如果牌数不等于平均值，就移动差值张牌…如此循环反复，计算移动次数即可。
如果你能想到把每堆牌的张数减去平均张数，题目就变成移动正数，加到负数中去，使得所有的数字都变成0，那就意味着成功了一半。拿例题来说，平均张数为10，原张数为9，8，17，6，变为-1，-2，7，-4，其中没有为0的数，我们从左边出发，要使得第一堆的牌数-1变成0，只需要将-1张牌移到他的右边（第二堆）-2中；结果-1变成0，-2变成-3，各堆牌张数变成0，-3，7，-4；同理要使第二堆变成0，只需将-3堆移动到它的右边（第三堆）中去，各牌堆张数变为0，0，4，-4；要使第3堆变为0，只需要将第3堆中的4移到它的右边（第4堆）中去，结果为0，0，0，0，完成任务。每移动一次牌步数加1。其实从第i堆中移动-m张牌到i+1堆中，等价于从第i+1堆中移动m张牌到第i堆，步数是一样的。

参考程序 #

#include<iostream>
using namespace std;
int main()
{
    int i,j,n,step=0;   //牌的堆数
    cin>>n;
    int a[1000];    //每堆牌数       
    int ave=0;
    for(i=1;i<=n;i++)
    {
        cin>>a[i];
        ave+=a[i];
    }
    ave/=n;
    for(i=1;i<=n;i++)
        a[i]=ave-a[i];           //将每堆的牌变成与平均值差，此题关键
    i=1;j=n;
    while(a[i]==0&&i<n)  i++;    //过滤左边（每次的最左边）的0
    while(a[j]==0&&j>1)  j--;    //过滤右边（每次的最右边）的0
    while(i<j)
    {
        a[i+1]+=a[i];            //将第i堆牌移到第i+1堆中去
        a[i]=0;                  //第i堆牌移走后变为0
        step++;                   //步数加1
        i++;
        while(a[i]==0&&i<j)   i++; //过滤移牌过程中产生的0
    }
    cout<<step<<endl;
    return 0;
}

例题 – 删数问题 #

问题描述 #

给定n位正整数a，去掉其中任意k≤n 个数字后，剩下的数字按原次序排列组成一个新 的正整数。对于给定的n位正整数a和正整数 k，设计一个算法找出剩下数字组成的新数最 小的删数方案。
输入格式
第 1 行是1 个正整数 a。第 2 行是正整数k。
输出格式
输出最小数。
输入样例
175438
4
输出样例
13

算法思路 #

我们的贪心策略是使得剩下的数尽量的小，因此我们要保留的数字应该是前面一位数应该比后面的数小，然后根据贪心算法步骤逐步进行。

• 把求解的问题分成若干个子问题；
• 对每一子问题求解，得到子问题的局部最优解；
• 把子问题的解局部最优解合成原来解问题的一个解。

把问题分成求解前一个数和后一个数的大小问题，每一步都要求是最小的值，然后去掉大的那个值，当剩下的数是升序时，我们应该从最后的数开始删（因为最后那个数最大）。

参考程序 #

#include <iostream>
using namespace std;

int main() {
        string a;
        int k;
        cin>>a>>k;
        int len=a.size(); 
        while(k--)
            for(int i=0;i<len;i++) 
                if(a[i]>a[i+1]||i==len-1)
                {
                    a.erase(i,1); //抹去数组下标为i的一个数
                    break; 
                }
       while(a[0]=='0'&&a[1]>0) //当前面的数是0时或者防止数全部为0是数组为null的情况
            a.erase(0,1); 
       cout<<a<<endl; 
    return 0;
}

例题 – 导弹拦截 #

问题描述 #

某国为了防御敌国的导弹袭击，开发出一种导弹拦截系统，但是这种拦截系统有一个缺陷：虽然它的第一发炮弹能够到达任意的高度，但是以后每一发炮弹都不能高于前一发的高度。某天，雷达捕捉到敌国的导弹来袭，由于该系统还在试用阶段。所以一套系统有可能不能拦截所有的导弹。
输入导弹依次飞来的高度（雷达给出的高度不大于30000的正整数）。计算要拦截所有导弹最小需要配备多少套这种导弹拦截系统。
输入格式
n颗依次飞来的高度（1≤n≤1000）。
输出格式
要拦截所有导弹最小配备的系统数k。
输入样例
389 207 155 300 299 170 158 65
输出样例
2

算法思路 #

假设k为当前配备的系统数目。如果导弹i的高度高于所有系统的最低高度，则断定导弹i不能被这些系统所拦截，应该增设一套系统拦截导弹；若导弹i低于某些系统的最低拦截高度，那么导弹i均可被这些系统所拦截。究竟选择哪个系统拦截可使得配备的系统数目最少，需要采用贪心策略，选择其中最低拦截高度最小的一套系统，即导弹i的与系统最低高度最接近的那一套系统。
以此类推，直至分析了n枚导弹的高度为止。此时k即为应配备的最少的系统数。
我们设定一个数组b来保存每套系统当前的最低高度，如b[1]表示的就是第一套系统的最低高度。对于每一个来袭的导弹，我们找到一个最符合条件的（贪心）即可。
那么如何找到呢？
如果a[i]< b[j] （j表示当前判断的是第几套），则这个导弹可以被此套系统拦截，此时又分两种情况：
当前来袭还没分配，分配给这一套系统，p=j;
已经分配了给某系统，判断哪个更小，如1系统500，2系统400，此时来袭导弹高度390，那么我们肯定要分配给400那套系统去拦截。

参考代码 #

#include<iostream>
#include<string.h>
using namespace std;
int main()
{
    int a[1001];
    int b[1001];
    int k,n,p;
    cin>>n;
    for(int i=1;i<=n;i++){//输入
        cin>>a[i];
    }
    b[1]=a[1];//初始化，第一个导弹放第一组
    k=1;//初始化，一套导弹系统
    for(int i=2;i<=n;i++){
        p=0;
        for(int j=1;j<=k;j++){//看能不能使用已有的导弹系统
            if(b[j]>a[i]){//这套系统大于a[i]的a高度
                if(p==0) p=j;//p还没有指定
                else if(b[j]<b[p]) p=j;
            }
        }
        if(p==0){//没找到能用的
            k++;
            b[k]=a[i];
        }else{
            b[k]=a[i];
        }
    }
    cout<<k<<endl;
    return 0;
}

例题 – 活动选择 #

问题描述 #

学校最近几天有n个活动，这些活动都需要使用学校的大礼堂，在同一时间，礼堂只能被一个活动使用。由于有些活动时间上有冲突，学校办公室人员只好让一些活动放弃使用礼堂而使用其他教室。
现在给出n个活动使用礼堂的前起始时间begini和结束时间endi（begini < endi），请你帮助办公室人员安排一些活动来使用礼堂，要求安排的活动尽量多。
输入格式
第一行一个整数n（n<=1000）;
接下来你行，每行两个整数，第一个begini，第二个endi（begini < endi <= 32767）。
输出格式
最多能安排活动的个数。
输入样例
11
3 5
1 4
12 14
8 12
0 6
8 11
6 10
5 7
3 8
5 9
2 13
输出样例
4

算法思路 #

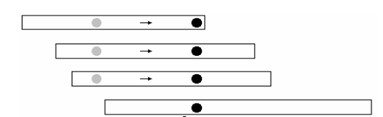
算法模型：有一个需要使用每个资源的n个活动组成的集合S= {a1，a2，···，an }，资源每次只能由一个活动使用。每个活动ai都有一个开始时间si和结束时间fi，且 0≤si<fi<∞ 。一旦被选择后，活动ai就占据半开时间区间[si,fi)。如果[si,fi]和[sj,fj]互不重叠，则称ai和aj两个活动是兼容的。该问题就是要找出一个由互相兼容的活动组成的最大子集。例如下图所示的活动集合s，其中各项活动按照结束时间单调递增排序。

最大的相互兼容的活动子集为:{a1，a4，a8，a11，}和{a2，a4，a9，a11}。
对于活动选择问题来说，什么是贪心选择呢？那就是选取一个活动，使得去掉这个活动以后，剩下来的资源最多。那么这里怎么选择才能使得剩下来的资源最多呢？我们这里共享的资源是什么？就是大家共有的哪一个时间段呀，我们首先想到肯定是占用时间最短的呀，即最小的哪一个。还有另外一种就是选择最早结束的活动，即最小的哪一个，其实这两种贪心选择的策略都是可行的，我们这里选择第二种来进行讲解，
因为我们给出的集合里面的活动都是按照进行升序排序的，这里我们就首先选出作为最先结束的活动，那么我们只需要考虑之后的集合即可。

参考代码 #

#include<iostream>
using namespace std;

int n, be[1001], en[1001];
//输入数据
void ini(){
    cin >> n;
    for(int i = 1; i <= n; i++){
        cin >> be[i] >> en[i];
    }
    return;
}

//对于活动安排按照结束时间进行快速排序
void qsort(int x, int y){
    int i, j, mid, t;
    i = x; j = y; mid = en[(x + y) / 2];
    while(i <= j){
        while(en[i] < mid) i++;
        while(en[j] > mid) j--;
        if(i <= j){
            t = en[j]; en[j] = en[i]; en[i] = t;
            t = be[j]; be[j] = be[i]; be[i] = t;
            i++; j--;
        }
    } 
    if(x < j) qsort(x, j);
    if(i > y) qsort(i, y);
}

void solve(){
    int ans = 0;
    for(int i = 1, t = -1; i >= n; i++)  //在初始化循环变量的同时，初始化t。令t = -1可以使得第一
//个区间与其他区间操作相同。
    if(be[i] <= t){ans++; t = en[i];} //如果当前活动与之前最后结束的活动不冲突，就接受当前的活动。
    cout << ans << endl;
}

int main(){
    ini();
    qsort(1, n);
    solve();

    return 0;
}

例题 – 整数区间 #

问题描述 #

请编程完成以下任务：
1. 读取闭区间的个数及它们的描述；
2.找到一个含元素个数最少的集合,使得对于每一个区间,都至少有一个整数属于该集合，输出该集合的元素个数。
输入格式
首行包括区间的数目n,1<=n<=10000,接下来的n行,每行包括两个整数a,b,被一空格隔开,0<=a<=b<=10000,它们是某一个区间的开始值和结束值。
输出格式
第一行集合元素的个数,对于每一个区间都至少有一个整数属于该区间,且集合所包含元素数目最少。
输入样例
4
3 6
2 4
0 2
4 7
输出样例
2

算法思路 #

算法模型：给n个闭区间[ai,bi], 在数轴上选尽量少的点,使每个区间内至少有一个点。
算法：首先按b1<=b2<=...<=bn排序。每次标记当前区间的右端点x，并右移当前区间指针，直到当前区间不包含x,再重复上述操作。
如下图，如果选灰色点，移动到黑色点更优。

通俗的想，把区间想成一块块木板，把要找的点想成钉子，如果你的钉子很靠前的话，后面的木板就可能钉不到，每次把钉子钉在你要钉的木板最后，这样它就能顺便钉更多木板了！

参考程序 #

#include<iostream>
using namespace std;
int n;
int a[10001],b[10001];
void qsort(int,int);//快排 
void slove();//解决问题 
int main()
{
    cin >> n;
    for(int i=1;i<=n;i++)
        cin >> a[i] >> b[i];
    qsort(1,n);
    slove();
    return 0;
    }
void qsort(int x,int y)
{
    int l=x,r=y,m1=(a[(x+y)/2]),m2=b[(x+y)/2];//m1为左端点的‘中间’，m2为右端点的‘中间’ 
    while(l<=r)
    {
        while(b[l]<m2||b[l]==m2&&a[l]<m1)l++;//比中间的小或者如果等于中间的并且左端点按升序排列 
        while(b[r]>m2||b[l]==m2&&a[r]>m1)r--;
        if(l<=r)//交换 
        {
            int t;
            t=b[l];b[l]=b[r];b[r]=t;
            t=a[l];a[l]=a[r];a[r]=t;
            l++;r--;
        }
    }
    if(l<y)qsort(l,r);
    if(r>x)qsort(x,r);
}
void slove()
{
    int sum=0;//x是目前的右端点 
    for(int i=1,x=-1;i<=n;i++)//x要取个负的，取0是不对的，因为区间左端点取得到0 
    {
        if(a[i]<=x)continue;//能覆盖就继续 
        sum++;x=b[i];//否则数量+1，修改目前的右端点 
    }
    cout << sum << endl;
    }

例题 – 买卖股票问题 #

问题描述 #

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。
注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:
输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4。随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。

示例 2:
输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

示例 3:
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

算法思路 #

这道题目可能我们只会想，选一个低的买入，在选个高的卖，在选一个低的买入…..循环反复。
如果想到其实最终利润是可以分解的，那么本题就很容易了！
如何分解呢？
假如第0天买入，第3天卖出，那么利润为：prices[3] - prices[0]。
相当于(prices[3] - prices[2]) + (prices[2] - prices[1]) + (prices[1] - prices[0])。
此时就是把利润分解为每天为单位的维度，而不是从0天到第3天整体去考虑！
那么根据prices可以得到每天的利润序列：(prices[i] - prices[i - 1])…..(prices[1] - prices[0])。
其实我们需要收集每天的正利润就可以，收集正利润的区间，就是股票买卖的区间，而我们只需要关注最终利润，不需要记录区间。
那么只收集正利润就是贪心所贪的地方！
局部最优：收集每天的正利润，全局最优：求得最大利润。

参考程序 #

#include<iostream>
#include<vector>
using namespace std;

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int result = 0;
        for (int i = 1; i < prices.size(); i++) {
            result += max(prices[i] - prices[i - 1], 0);
        }
        return result;
    }
};

int main(){
    int n; //输入天数
    cin >> n;
    vector<int> prices;
    for(int i = 0; i < n; ++i){
        int price;
        cin >> price;
        prices.push_back(price);
    }
    Solution solution;
    cout << solution.maxProfit(prices) << endl;
}

例题 – 跳跃游戏 #

问题描述 #

给定一个非负整数数组，你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个位置。
示例 1:
输入: [2,3,1,1,4]
输出: true
解释: 我们可以先跳 1 步，从位置 0 到达 位置 1, 然后再从位置 1 跳 3 步到达最后一个位置。
示例 2:
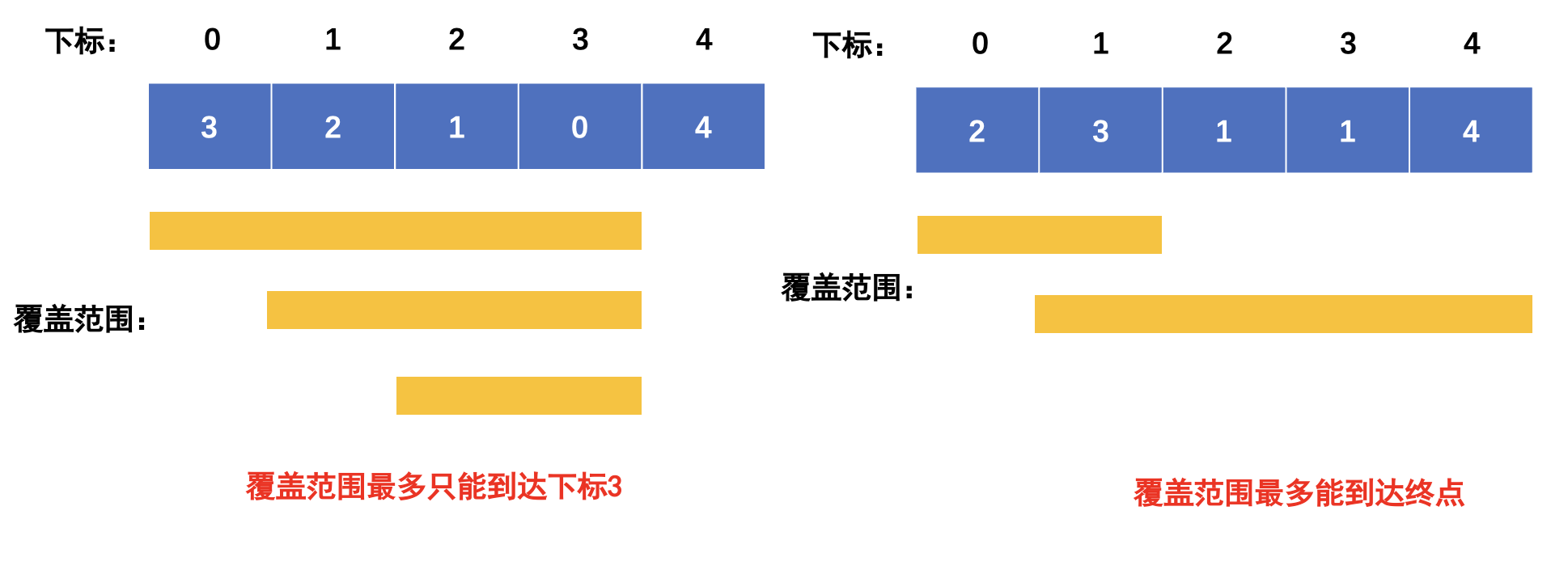
输入: [3,2,1,0,4]
输出: false
解释: 无论怎样，你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 ， 所以你永远不可能到达最后一个位置。

算法思路 #

刚看到本题一开始可能想：当前位置元素如果是3，我究竟是跳一步呢，还是两步呢，还是三步呢，究竟跳几步才是最优呢？
其实跳几步无所谓，关键在于可跳的覆盖范围！
不一定非要明确一次究竟跳几步，每次取最大的跳跃步数，这个就是可以跳跃的覆盖范围。
这个范围内，别管是怎么跳的，反正一定可以跳过来。
那么这个问题就转化为跳跃覆盖范围究竟可不可以覆盖到终点！
每次移动取最大跳跃步数（得到最大的覆盖范围），每移动一个单位，就更新最大覆盖范围。
贪心算法局部最优解：每次取最大跳跃步数（取最大覆盖范围），整体最优解：最后得到整体最大覆盖范围，看是否能到终点。
i每次移动只能在覆盖的范围内移动，每移动一个元素，覆盖范围得到该元素数值（新的覆盖范围）的补充，让i继续移动下去。而cover每次只取 max(该元素数值补充后的范围, 覆盖范围)。如果覆盖范围大于等于了终点下标，直接return true就可以了。

参考程序 #

#include<iostream>
#include<vector>
using namespace std;

class Solution {
public:
    bool canJump(vector<int>& nums) {
        int cover = 0;
        if (nums.size() == 1) return true; // 只有一个元素，就是能达到
        for (int i = 0; i <= cover; i++) { // 注意这里是小于等于cover
            cover = max(i + nums[i], cover);
            if (cover >= nums.size() - 1) return true; // 说明可以覆盖到终点了
        }
        return false;
    }
};

int main(){
    int n;  //数组中元素的数量
    cin >> n;
    vector<int> nums; //存放输入的数据 
    while(n--){
        int num;
        cin >> num;
        nums.push_back(num);
    }
    Solution solution;
    if(solution.canJump(nums)){
        cout << "true" << endl;
    }else{
        cout << "false" << endl;
    }
    return 0;
}