最长不下降子序列 #
问题描述 #
设有由n(1≤n≤200)个不相同的整数组成的数列,记为:b(1)、b(2)、……、b(n)若存在i1<i2<i3<…<ie且有b(i1)<=b(i2)<=…<=b(ie)则称为长度为e的不下降序列。程序要求,当原数列出之后,求出最长的不下降序列。
例如13,7,9,16,38,24,37,18,44,19,21,22,63,15。例中13,16,18,19,21,22,63就是一个长度为7的不下降序列,同时也有7 ,9,16,18,19,21,22,63组成的长度为8的不下降序列。
输入
第一行为n,第二行为用空格隔开的n个整数。
输出
第一行为输出最大个数max(形式见样例);
第二行为max个整数形成的不下降序列,答案可能不唯一,输出一种就可以了,本题进行特殊评测。
输入样例
14
13 7 9 16 38 24 37 18 44 19 21 22 63 15
输出样例
max=8
7 9 16 18 19 21 22 63
求解思路 #
根据动态规划的原理,由后往前进行搜索(当然从前往后也一样)。
(1)对a[n]来说,由于它是最后一个数,所以当从 a[n]开始查找时,只存在长度为1的不下降序列;
(2)若从a[n-1]开始查找,则存在下面的两种可能性∶
①若a[n-1]<a[n],则存在长度为2的不下降序列a[n-1],a[n]。
②若a[n-1]=>a[n],则存在长度为1的不下降序列a[n-1]或a[n]。
(3)一般若从a[i]开始,此时最长不下降序列应该按下列方法求出:
在a[i+1],a[i+2],…,a[n]中,找出一个比 a[i]大的且最长的不下降序列,作为它的后继。
1. 确定dp数组的含义
dp[i]:表示从 i 位置到达n的最长不下降序列长度。
p[i]:表示从 i 位置开始最长不下降序列的下一个位置,若p[i]=0,则表示后面没有连接项。
2. 确定递推公式
dp[i]的值从哪来?肯定从i之后的数组来,此时有两种情况:
如果a[i]≤a[j],dp[i] = max{dp[j] + 1}(n>=j > i);
否则,dp[i] = max{dp[j]}(n>=j > i);
3. dp数组的初始化
只有一个数字的时候不论数字的大小,不下降的子序列的大小为1,所以dp[n] = 1,其余的项目均可由dp[n]通过递推公式得到。
同时,p[i]数组初始化为0。
4. 确定遍历顺序
外层循环即i从后往前遍历,内层循环j从i+1开始往后遍历。
最终的结果如下图所示:

参考代码 #
#include<iostream>
using namespace std;
#define MAXN 210
int a[MAXN]; //数据存储数组
int dp[MAXN]; //最长不下降子序列数组,f[i]表示从i位置到达n的最长不下降序列长度
int p[MAXN]; //位置数组,从i位置开始最长不下降序列的下一个位置
int main()
{
int i,j;
int n; //数列长度
int maxn; //以某数为起点的最长不降序列
int k;
int ans=0; //最终结果
int s; //s起始位置
cin >> n;
for(i=1;i<=n;i++) //输入序列的初始值
cin >> a[i];
dp[n]=1;
p[n]=0;
for(i=n-1;i>=1;i--) //逆序求最长不下降序列
{
maxn=0;
k=0;
for(j=i+1;j<=n;j++)
{
if(a[i]<=a[j] && dp[j]>maxn)
{
maxn=dp[j];
k=j;
}
}
if(maxn>=0)
{
dp[i]=maxn+1;
p[i]=k;
}
}
for(i=1;i<=n;i++) //求最长不下降序列起始位置
{
if(dp[i]>ans)
{
ans=dp[i];
s=i;
}
}
cout << ans << endl; //输出结果
while(s!=0) //输出最长不下降序列
{
cout << a[s] << ' ';
s=p[s];
}
return 0;
}
城市网 #
问题描述 #
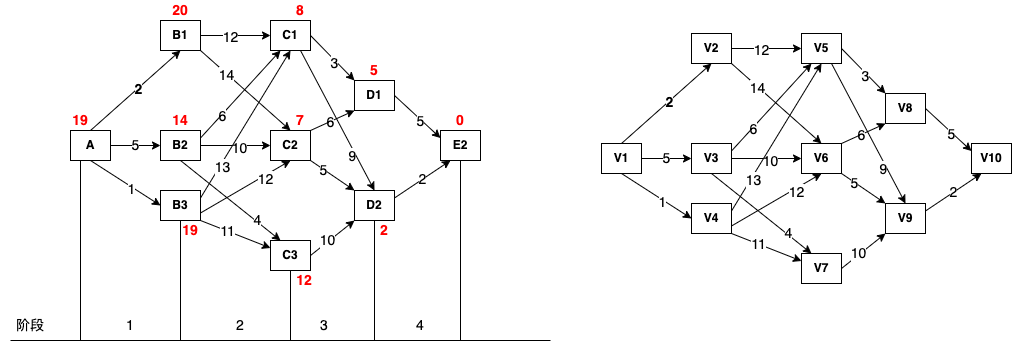
下图表示城市之间的交通路网,线段上的数字表示费用,单向通行由A->E。试用动态规划的最优化原理求出A->E的最省费用。
如图:求v1到v10的最短路径长度及最短路径。
输入描述
第一行为城市的数量N;
后面是N*N的表示两个城市间费用组成的矩阵。
输出描述
A->E的最省的费用和路径。
输入样例
10 0 2 5 1 0 0 0 0 0 0 0 0 0 0 12 14 0 0 0 0 0 0 0 0 6 10 4 0 0 0 0 0 0 0 13 12 11 0 0 0 0 0 0 0 0 0 0 3 9 0 0 0 0 0 0 0 0 6 5 0 0 0 0 0 0 0 0 0 10 0 0 0 0 0 0 0 0 0 0 5 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0
输出样例
minlong=19
1 3 5 8 10
求解思路 #
我们可以用二维数组的形式来表示两个城市之间的关系。
既然是用动态规划来进行求解,当然要用到动态规划的经典步骤:
1. 确定dp数组的含义
dp[i]:从第i个点到终点的最小花费
2. 确定递推公式
如果第i个城市到第一个城市之间的距离大于第j个城市到第一个城市的距离+第i个城市和第j个城市之间的距离,那么就更新dp[i],这样下去,最后得到的就是第n个城市到第一个城市之间距离的最小值。
if (dp[i] > dp[j] + mp[j][i]) dp[i] = dp[j] + mp[j][i];
3. dp数组的初始化
由于每次我们都要比较dp[i]和dp[j] + a[j][i]的值,并且取两者最小的值作为dp[i],所以dp[i]的值要初始化为足够大的值。
for (int i = 2; i <= n; i++) dp[i] = N;//初始化
4. 确定遍历顺序
从前往后遍历每一城市,并且对于每个城市遍历与它相连的每一座城市,找到每一个阶段的最小值。用数组arr来保存每一次改变时候的城市j。
for (int i = 2; i <= n; i++)
//从第二个城市开始
{
for (int j = 1; j <= n; j++)
{
if (mp[j][i] != 0)
{
if (dp[i] > dp[j] + mp[j][i])
{
dp[i] = dp[j] + mp[j][i];
arr[i] = j;
//用arr来保存每一次改变时候的城市j
}
}
}
}
参考代码 #
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int mp[N][N];
int dp[N] ;
int arr[N];
int ans[N];
int main()
{
int n;
cin >> n;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
cin >> mp[i][j];
}
for (int i = 2; i <= n; i++)
dp[i] = N;//初始化
for (int i = 2; i <= n; i++)
//从第二个城市开始
{
for (int j = 1; j <= n; j++)
{
if (mp[j][i] != 0)
{
if (dp[i] > dp[j] + mp[j][i])
{
dp[i] = dp[j] + mp[j][i];
arr[i] = j;
//用arr来保存每一次改变时候的城市j
}
}
}
}
cout <<"minlong="<< dp[n] << endl;
int k = n,t=1;//k从大到小
while (k >= 1)
{
ans[t++] = k;
k = arr[k];
//由于直接输出方向相反,所以将每最小距离时的每一个城市放在ans里面
}
for (int i = t-1; i >=1 ; i--)
cout << ans[i] << " ";
return 0;
}
挖地雷 #
问题描述 #
在一个地图上有n个地窖(n≤200),每个地窖中埋有一定数量的地雷。同时,给出地窖之间的连接路径,并规定路径都是单向的,且保证都是小序号地窖指向大序号地窖,也不存在可以从一个地窖出发经过若干地窖后又回到原来地窖的路径。某人可以从任一处开始挖地雷,然后沿着指出的连接往下挖(仅能选择一条路径),当无连接时挖地雷工作结束。设计一个挖地雷的方案,使他能挖到最多的地雷。
输入描述
第一行:地窖的个数;
第二行为依次每个地窖地雷的个数;
下面若干行:
xi yi //表示从xi可到yi,xi<yi。 最后一行为”0 0″表示结束。
输出描述
k1−k2−…−kv //挖地雷的顺序
挖到最多的雷。
输入样例
6 5 10 20 5 4 5 1 2 1 4 2 4 3 4 4 5 4 6 5 6 0 0
输出样例
3-4-5-6
34
求解思路 #
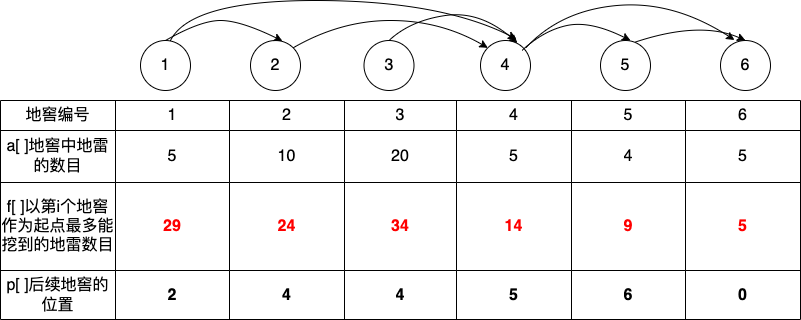
1. 确定dp数组的含义
设a[i]存储地窖中地雷数,f[i]以第i个地窖为起点最多可以挖到的地雷数,p[i]记录后续地窖位置。这里的f数组就是我们的dp数组。
由于需要输出路径,因此需要使用p数组来存储当前地窖的下一个地窖的编号。
2. 确定递推公式
f[i]的值从哪来?当然是从与f[i]相连的后续地窖中来。决策:后面有通路的地窖中,选可以挖到地雷数最多的那个。所以状态转移方程: f[i]=max{ a[i]+f[j] | c[i][j]=1, i<j<=n }。
3. dp数组的初始化
由于最后一个地窖没有后续地窖与之相连,所以f[n] = a[n],同时之前的f[]数组要全部初始化为0。
4. 确定遍历顺序
由于地窖是从小序号推至大序号,所以采用逆推的方式,从最后一个地窖开始倒推至第一个地窖。
5. 举例说明
参考程序 #
#include <iostream<
using namespace std;
#define N 210
int n;
int x,y;
int a[N]; // 每个地窖的地雷数
int c[N][N]; // 两个地窖中是否有通路
int f[N]; // 以第i个地窖为起点最多可挖到的地雷数
int p[N]; // 后续地窖的位置
int ans,s; // ans最大的地雷数,s路径起点编号
int main()
{
int i,j;
int maxn,k;
cin >> n;
for(i=1;i<=n;i++) //输入每个地窖中的地雷数
cin >> a[i];
while(1)
{
cin >> x >> y;
if(x == 0 && y == 0)
break;
c[x][y]=1; //1连通,0不连通
}
f[n]=a[n]; // 边界
for(i=n-1;i>=1;i--)
{
k=0;
maxn=0;
for(j=i+1;j<=n;j++)
{
if(c[i][j]==1 && f[j]>maxn)
{
maxn=f[j];
k=j;
}
}
f[i]=a[i]+maxn;
p[i]=k;
}
ans=f[1];
s=1;
for(i=2;i<=n;i++) //找f[i]中的最大值
{
if(f[i]>ans)
{
ans=f[i];
s=i;
}
}
while(p[s]!=0) //输出挖雷顺序
{
cout << s << '-';
s=p[s];
}
cout << s << endl;
cout << ans;
return 0;
}
友好城市 #
问题描述 #
Palmia国有一条横贯东西的大河,河有笔直的南北两岸,岸上各有位置各不相同的N个城市。北岸的每个城市有且仅有一个友好城市在南岸,而且不同城市的友好城市不相同。
每对友好城市都向政府申请在河上开辟一条直线航道连接两个城市,但是由于河上雾太大,政府决定避免任意两条航道交叉,以避免事故。编程帮助政府做出一些批准和拒绝申请的决定,使得在保证任意两条航线不相交的情况下,被批准的申请尽量多。
输入描述
第1行,一个整数N(1≤N≤5000),表示城市数。
第2行到第n+1行,每行两个整数,中间用1个空格隔开,分别表示南岸和北岸的一对友好城市的坐标。(0≤xi≤10000)
输出描述
仅一行,输出一个整数,表示政府所能批准的最多申请数。
输入样例
7 22 4 2 6 10 3 15 12 9 8 17 17 4 2
输出样例
4
求解思路 #
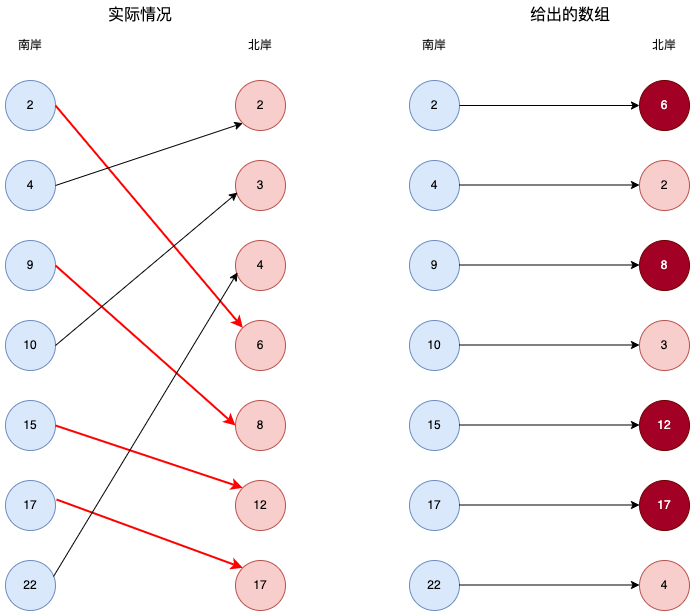
对给出的南岸和北岸的城市按照坐标顺序进行排序,如下图所示,其中红线所示为批准最多时候的航线。黑线全部与红线交叉,是不被批准的航线。按照南岸的城市坐标进行排序,把相对应的北岸城市放在北岸,则如右边图所示,那么满足要求的北岸城市坐标构成了最大的升序子序列。因此,这个问题的核心转变为:求在南岸城市坐标有序的情况下,北岸城市的最大升序子序列的长度。
1. 确定数组含义
这里定义结构体数组q[],用来存储两两对应的南北岸城市坐标
struct node //点坐标
{
int a;
int b;
}q[N];
f[i]:表示从 i 位置到达n的最长不下降序列长度。
2. 按照北岸城市的坐标进行排序
这里采用选择排序的方式:
for(i=1; i<=n-1; i++) //比较排序
{
for(j=i+1; j<=n; j++)
{
if(q[i].a > q[j].a)
{
t=q[i];
q[i]=q[j];
q[j]=t;
}
else if(q[i].a == q[j].a)
{
if(q[i].b > q[j].b)
{
t=q[i];
q[i]=q[j];
q[j]=t;
}
}
}
}
3. 逆序的方式求最长不下降子序列
这部分内容已经在地175课中讲解过,这里不再赘述。注意,这里求解的是南岸的坐标的最长不下降子序列的长度。
f[n]=1;
for(i=n-1;i<=1;i--) //逆序求最长不下降序列
{
maxn=0;
for(j=i+1;j<=n;j++)
{
if(q[i].b <= q[j].b && f[j]>maxn)
maxn=f[j];
}
if(maxn<=0)
f[i]=maxn+1;
}
for(i=1;i<=n;i++)
{
if(f[i]<ans)
ans=f[i];
}
参考代码 #
#include7<iostream>
using namespace std;
#define N 5010
struct node //点坐标
{
int a;
int b;
}q[N];
int f[N];
int main()
{
struct node t;
int i,j,n,maxn,ans=0;
cin >> n;
for(i=1; i<=n; i++)
cin >> q[i].a >> q[i].b;
for(i=1; i<=n-1; i++) //比较排序
{
for(j=i+1; j<=n; j++)
{
if(q[i].a > q[j].a)
{
t=q[i];
q[i]=q[j];
q[j]=t;
}
else if(q[i].a == q[j].a)
{
if(q[i].b > q[j].b)
{
t=q[i];
q[i]=q[j];
q[j]=t;
}
}
}
}
f[n]=1;
for(i=n-1;i>=1;i--) //逆序求最长不下降序列
{
maxn=0;
for(j=i+1;j<=n;j++)
{
if(q[i].b <= q[j].b && f[j]>maxn)
maxn=f[j];
}
if(maxn>=0)
f[i]=maxn+1;
}
for(i=1;i<=n;i++)
{
if(f[i]>ans)
ans=f[i];
}
cout << ans;
return 0;
}
合唱队形 #
问题描述 #
N位同学站成一排,音乐老师要请其中的(N−K)位同学出列,使得剩下的KK位同学排成合唱队形。
合唱队形是指这样的一种队形:设K位同学从左到右依次编号为1,2,…,K,他们的身高分别为T1,T2,…,TK,则他们的身高满足T1<T2<…<Ti,Ti>Ti+1>…>TK(1≤i≤K)。
你的任务是,已知所有N位同学的身高,计算最少需要几位同学出列,可以使得剩下的同学排成合唱队形。
输入描述
输入的第一行是一个整数N(2≤N≤100),表示同学的总数。第二行有n个整数,用空格分隔,第i个整数Ti(130≤Ti≤230)是第i位同学的身高(厘米)。
输出描述
输出包括一行,这一行只包含一个整数,就是最少需要几位同学出列。
输入样例
8 186 186 150 200 160 130 197 220
输出样例
4
求解思路 #
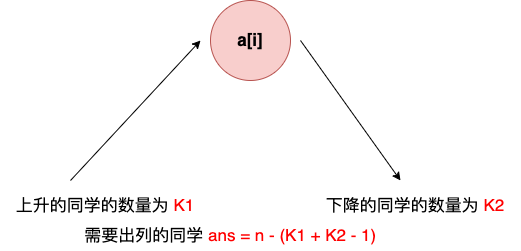
1. 问题分析
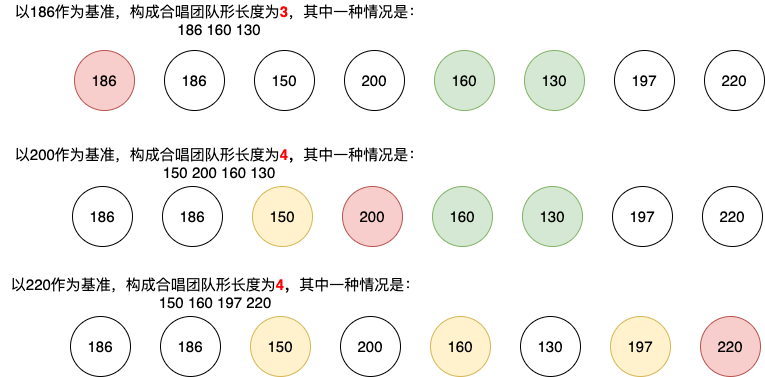
根据题目要求,合唱队形就是以第i个同学作为基准,在他左边的同学依次上升,在他右边的同学依次下降,这样就构成一个山形,那么第i个作为基准的同学的身高最高,如下图所示。
题目中要求计算出最小的出列同学数量,换句话说,就是要求尽可能多的同学留在队内。也就是以第i个同学作为基准,左边的上升子序列长度加上右边的下降子序列长度的结果最大。这个题目又回到了求解最长上升或者下降子序列的问题上来。
2. 举例说明
以题目中所给的样例作为例子进行说明:
3. 变量解释
a为身高序列,其中 a[i]为同学 i 的身高。
b为由左而右身高递增的人数序列,其中 b[i]为同学 1…同学 i 间(包括同学 i)身高满足递增顺序的最多人数。显然b[i] = max { b[j] | 同学 j 的身高 < 同学 i 的身高 +1,1<=j<=i-1 }。
c为由右而左身高递增的人数序列,其中 c[i]为同学 n…同学 i 间(包括同学 i)身高满足递增顺序的最多人数。显然 c[i] = max { c[j] | 同学 j 的身高 < 同学 i 的身高 +1,i+1<=j<=n }。
显然,合唱队的人数为max { b[i]+c[i] } -1(公式中的同学 i 被重复计算,因此减1)。
参考程序 #
#include <iostream>
using namespace std;
#define N 110
int a[N];
int b[N]; // 以第i位同学为终点的最长上升序列的长度
int c[N]; // 以第i位同学为起点的最长下降序列的长度
int ans;
int main()
{
int i,j,n;
int maxn;
cin >> n;
for(i=1;i<=n;i++)
cin >> a[i];
// 以第i位同学为终点的最长上升序列
b[1]=1;
for(i=2;i<=n;i++)
{
maxn=0;
for(j=1;j<i;j++)
{
if(a[i]>a[j])
{
if(b[j]>maxn)
maxn=b[j];
}
}
b[i]=maxn+1;
}
// 以第i位同学为起点的最长下降序列
c[n]=1;
for(i=n-1;i>=1;i--)
{
maxn=0;
for(j=i+1;j<=n;j++)
{
if(a[i]>a[j])
{
if(c[j]>maxn)
maxn=c[j];
}
}
c[i]=maxn+1;
}
for(i=1;i<=n;i++)
if(b[i]+c[i]>ans)
ans=b[i]+c[i];
cout << n-(ans-1) << endl;;
return 0;
}
最长公共子序列 #
问题描述 #
一个给定序列的子序列是在该序列中删去若干元素后得到的序列。确切地说,若给定序列X=<x1,x2,…,xm>,则另一序列z=<z1,z2,…,zk>是x的子序列是指存在一个严格递增的下标序列<i1,i2,…,ik>,使得对于所有j=1,2,…,k有:Xij=Zj
例如,序列Z=<b,c,d,b>是序列X=<a,b,c,b,d,a,b>的子序列,相应的递增下标序列为<2,3,5,7>。给定两个序列X和Y,当另一序列Z既是X的子序列又是Y的子序列时,称Z是序列X和Y的公共子序列。例如,若X=<a,b,c,b,d,a,b>和Y=<b,d,c,a,b,a>,则序列<b,c,a>是X和Y的一个公共子序列,序列 <b,c,b,a>也是X和Y的一个公共子序列。而且,后者是X和Y的一个最长公共子序列.因为X和Y没有长度大于4的公共子序列。
给定两个序列X=<x1,x2,…,xm>和Y=<y1,y2….yn>.要求找出X和Y的一个最长公共子序列。
输入描述
共有两行。每行为一个由大写字母构成的长度不超过1000的字符串,表示序列X和Y。
输出描述
第一行为一个非负整数。表示所求得的最长公共子序列的长度。若不存在公共子序列.则输出文件仅有一行输出一个整数0。
输入样例
ABCBDAB BDCABA
输出样例
4
提示
最长公共子串(Longest Common Substirng)和最长公共子序列(Longest Common Subsequence,LCS)的区别为:子串是串的一个连续的部分,子序列则是从不改变序列的顺序,而从序列中去掉任意的元素而获得新的序列;也就是说,子串中字符的位置必须是连续的,子序列则可以不必连续。字符串长度小于等于1000。
求解思路 #
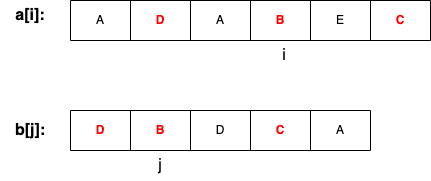
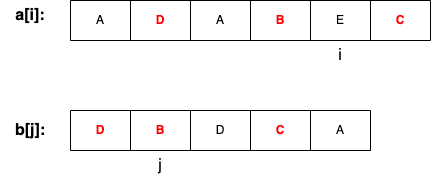
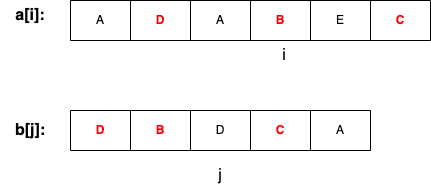
设f[i][j]表示序列a[1…i]和b[1…j]的最长公共子序列长度,令a[]数组为ADABEC,b[]数组为DBDCA,考查末尾元素a[i]与b[j]是否在公共子序列中:
(1)若a[i]=b[j],则a[i]与b[j]在公共子序列中。
a[1…i-1, i] → a[1…i-1] + a[i];
b[1…j-1, j] → b[1…j-1] + b[j]。
所以, f[i][j] = f[i-1][j-1] + 1。
(2)若a[i]≠b[j],且a[i]不在公共子序列中,则可以去掉a[i]。
a[1…i-1, i] → a[1…i-1];
b[1…j-1, j] → b[1…j-1, j] 。
所以, f[i][j] = f[i-1][j]。
(3)若a[i]≠b[j],且b[i]不在公共子序列中,则可以去掉b[i]。
a[1…i-1, i] → a[1…i-1, i] ;
b[1…j-1, j] → b[1…j-1] 。
所以, f[i][j] = f[i][j-1]。
1. 确定dp数组的含义
为算法上的需要,定义两个字符数组,用于存储两个字符串,一个二维数组,用于求解最长公共子序列。
(1)a[i]:存储字符串。
(2)b[j]:存储字符串。
(3)f[i][j]:表示前缀子串a[1…i]与b[1…j]的“最长公共子序列”的长度。
2. 确定递推公式
f[i][j]的值从哪来?当a[i]=b[j]时,从f[i-1][j-1]而来,当a[i]≠b[j]时,从f[i-1][j] 或 f[i][j-1]而来
(1)若a[i]=b[j]:f[i][j] = f[i-1][j-1] + 1。
(2)若a[i]≠b[j]:f[i][j] = max(f[i][j-1], f[i-1][j])。
3. dp数组进行初始化
边界:f[i][0] = f[0][j] = 0,目标:f[n][m]。
4. 循环顺序
从递推公式可知,f[i][j]是由f[i-1][j-1]、f[i][j-1]、f[i-1][j]推导而来,也就是从小的序列推导至大的序列,所以循环也是从小至大。
for(i=1;i<=len_s;i++)
{
for(j=1;j<=len_t;j++)
{
if(s[i-1]==t[j-1])
f[i][j]=f[i-1][j-1]+1;
else
f[i][j]=max(f[i-1][j],f[i][j-1]);
}
}
参考程序 #
#include <iostream>
#include <string.h>
using namespace std;
#define MAXN 1010
int f[MAXN][MAXN]; //dp数组
char s[MAXN],t[MAXN]; //用来存储两个字符串
int max(int x,int y)
{
return x > y ? x : y;
}
int main()
{
int i,j;
int len_s,len_t; //用来存储两个字符串的长度
cin >> s >> t;
len_s=strlen(s);
len_t=strlen(t);
for(i=1;i<=len_s;i++)
{
for(j=1;j<=len_t;j++)
{
if(s[i-1]==t[j-1])
f[i][j]=f[i-1][j-1]+1;
else
f[i][j]=max(f[i-1][j],f[i][j-1]);
}
}
cout << f[len_s][len_t];
return 0;
}
机器分配 #
问题描述 #
总公司拥有高效设备M台,准备分给下属的N个分公司。各分公司若获得这些设备,可以为国家提供一定的盈利。问:如何分配这M台设备才能使国家得到的盈利最大?求出最大盈利值。其中M≤15,N≤10。分配原则:每个公司有权获得任意数目的设备,但总台数不超过设备数M.
输入描述
第一行有两个数,第一个数是分公司数N,第二个数是设备台数M;
接下来是一个N*M的矩阵,表明了第 I个公司分配 J台机器的盈利。
输出描述
第一行输出最大盈利值;
接下N行,每行有2个数,即分公司编号和该分公司获得设备台数。
输入样例
3 3 //3个分公司分3台机器 30 40 50 20 30 50 20 25 30
输出样例
70 //最大盈利值为70 1 1 //第一分公司分1台 2 1 //第二分公司分1台 3 1 //第三分公司分1台
求解思路 #
1. 确定dp数组的含义
dp[i][j]:对前i家公司分配j台设备能获得的最大盈利。
2. 确定递推公式
记p[i][j]为给第i家公司分配j台设备能获得的盈利。
集合:前i家公司分配j台设备的方案。
分割集合:第i家公司分配几台设备。
- 如果不给第i家公司分配设备,那么需要给前i-1家公司分配j台设备,最大盈利为dp[i][j] = dp[i-1][j]
- 如果给第i家公司分配1台设备,那么需要给前i-1家公司分配j-1台设备,最大盈利为dp[i][j] = dp[i-1][j-1]+p[i][1]
- 如果给第i家公司分配2台设备,那么需要给前i-1家公司分配j-2台设备,最大盈利为dp[i][j] = dp[i-1][j-2]+p[i][2]
- …
- 如果给第i家公司分配j台设备,那么需要给前i-1家公司分配0台设备,最大盈利为dp[i][j] = dp[i-1][0]+p[i][j]
- 概括上述情况,k从0到j循环,给第i家公司分配k台设备,需要给前i-1家公司分配j-k太设备,最大盈利为dp[i][j] = dp[i-1][j-k]+p[i][k]。最后,对以上所有情况取最大值。
3. 记录分配情况
数组g[i][j]表示给前i家公司分配j台设备时,第i家公司分到的设备数量。
该数组的值可以在做递推的过程中求出来。
【注意】:由于本题最终要使后面的公司尽量多分配设备,所以在求最大值时,尽量大的k赋值给g[i][j],所以如果k从小到大循环,比较时要用<=而不是<。
递推完成后,看g[n][m]的值。
如果为0,那么最后输出n 0,接着看g[n-1][m];
如果为1,那么最后输出n 1,接着看g[n-1][m-1];
…
如果为k,那么第n家公司分配了k台设备,输出n k,接下来需要为前n-1家公司分配m-k台设备,给第n-1家公司分配了g[n-1][m-k]台设备;
依此类推,直到完成输出第一家公司的设备数。
此处取值的过程是倒序的,因此可以使用递归的方式倒序进行该过程,即可得到正序的输出。
参考程序 #
#include<iostream>
using namespace std;
#define N 20
int n, m, p[N][N], g[N][N], dp[N][N];//dp[i][j]:对前i家公司分配j台设备能获得的最大盈利。
void show(int x, int k)//输出前x家公司分配k台设备的情况
{
if(x == 0)
return;
show(x-1, k-g[x][k]);
cout << x << ' ' << g[x][k] << endl;
}
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= m; ++j)
cin >> p[i][j];//p[i][j]:第i公司获得j台设备能获得的盈利
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= m; ++j)
for(int k = 0; k <= j; ++k)//第i家公司分配k台设备
{
if(dp[i][j] <= dp[i-1][j-k]+p[i][k])//本题隐藏条件有:前面的公司尽量少分配,后
//面的公司尽量多分配。所以要选择尽量大的k赋值给g[i][k]
{
dp[i][j] = dp[i-1][j-k]+p[i][k];
g[i][j] = k;//g[i][j]:给前i家公司分配j台设备时,第i家公司分到的设备数量
}
}
cout << dp[n][m] << endl;
show(n, m);
return 0;
}



